Ch 07 Symmetric Matrices and Quadratic Forms

7.4 The Singular Value Decomposition (1)

The diagonalization theorems in Sections 5.3 and 7.1 play a part in many interesting applications. Unfortunately, as we know, not all matrices can be factored as $A=PDP^{-1}$ with D diagonal. However, a factorization $A=QDP^{-1}$ is possible for any $m \times n$ matrix A! A special factorization of this type, called the singular value decomposition, is one of the most useful matrix factorizations in applied linear algebra.

The singular value decomposition is based on the following property of the ordinary diagonalization that can be imitated for rectangular matrices: The absolute values of the eigenvalues of a symmetric matrix $A$ measure the amounts that $A$ stretches or shrinks certain vectors (the eigenvectors).

If $A\textbf{x}=\lambda\textbf{x}$ and $||\textbf{x}||=1$, then

$$\begin{align} || A \textbf{x} || &= || \lambda \textbf{x} || \\ &= | \lambda | || \textbf{x} || \\ &= | \lambda | \tag{1} \end{align}$$

If $\lambda_1$ is the eigenvalue with the greatest magnitude, then a corresponding unit eigenvector $\textbf{v}_1$ identifies a direction in which the stretching effect of $A$ is greatest. That is, the length of $A\textbf{x}$ is maximized when $\textbf{x}_1=\textbf{v}_1$, and $||A\textbf{v}_1||=|\lambda_! ||$, by (1). This description of $\textbf{v}_1$ and $|\lambda_1 |$ has an analogue for rectangular matrices that will lead to the singular value decomposition.

Example 1

If $A=\begin{bmatrix} 4 & 11 & 14 \\ 8 & 7 && -2 \end{bmatrix}$, then the linear transformation $\textbf{x} \mapsto A\textbf{x}$ maps the unit sphere $\left\{ \textbf{x}: ||\textbf{x}||=1\right\}$ in $\mathbb{R}^3$ onto an ellipse in $\mathbb{R}^2$, shown figure 1. Find a unit vector $\textbf{x}$ at which the length $||A\textbf{x}||$ is maximized, and compute this maximum length.

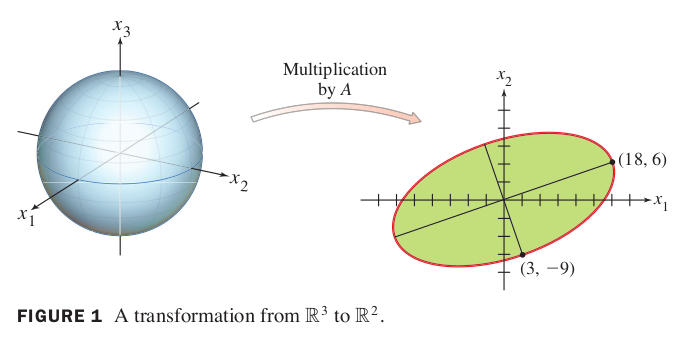
Solution of Example 1

Example 1 suggests that the effect of $A$ on the unit sphere in $\mathbb{R}^3$ is related to the quadratic form $\textbf{x}^TA\textbf{x}$. In fact, the entire geometric behavior of the transformation $\textbf{x} \mapsto A\textbf{x}$ is captured by this quadratic form, as we shall see.

The Singular Values of an $m$ by $n$ Matrix

Let $A$ be an $m \times n$ matrix. Then $A^TA$ is symmetric and can be orthogonally diagonlized. Let $\left\{ \textbf{v}_1 \cdots \textbf{v}_n \right\}$ be an orthonormal basis for $\mathbb{R}^n$ consisting of eigenvectors of $A^TA$, and let $\lambda_1, \cdots \lambda_n$ be the associated eigenvalue of $A^TA$. Then, for $1\le i\le n$,

$$\begin{align*} ||A\textbf{v}_i||^2 &= (A\textbf{v}_i)^TA\textbf{v}_i \\ &= \textbf{v}_i^T A^T \textbf{v}_i \\ &= \textbf{v}_i^T(\lambda_i \textbf{v}_i) & \text{Since }\textbf{v}_i\text{ is an eigenvector of }A^TA \\ &= \lambda_i &\text{Since }\textbf{v}_i\text{ is a unit vector} \tag{2} \end{align*}$$

So the eigenvalues fo $A^TA$ are all nonnegative. By renumbering, if necessary, we may assume that the eigenvalues are arranged so that

$$\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_n \ge 0$$

The singular values of $A^TA$ are the square roots of the eigenvalues of $A^TA$, denoted by $\sigma_1, \cdots, \sigma_n$, and they are arranged in decreaing order. That is, $\sigma_i = \sqrt{\lambda_i}$ for $1\le i \le n$.

By equation (2), *the singular values of $A$ are the lengths of the vectors $A\textbf{v}_1, \cdots A\textbf{v}_n$.

Theorem 9

Suppose $\left\{ \textbf{v}_1 \cdots \textbf{v}_n \right\}$ is an orthonormal basis of $\mathbb{R}^n$ consisting of eigenvectors of $A^TA$, arranged so that corresponding eigenvalues of $A^TA$ satisfy $\lambda_1 \ge \cdots \lambda_n$, and suppose $A$ has $r$ nonzero singular values. Then $\left\{ A\textbf{v}_1 \cdots A\textbf{v}_n \right\}$ is an orthogonal basis for $\text{Col} A$, and $\text{rank} A=r$

Proof of Theorem 9

Because $\textbf{v}_i$ and $\lambda_j \textbf{v}_j$ are orthogonal for $i \ne j$,

$$\begin{align*} (A\textbf{v}_i)^T(A\textbf{v}_j) &= \textbf{v}_i^T A^T A\textbf{v}_j \\ &=\textbf{v}_i)^T (\lambda_j \textbf{v}_j) \\ &=0 \end{align*}$$

Thus $\left\{ A\textbf{v}_1 \cdots A\textbf{v}_n \right\}$ is an orthogonal set. Furthermore, since the length of the voectors $A\textbf{v}_1 \cdots A\textbf{v}_n$ are the singular values of $A$, and since there are $r$ nonzero singular vectors, $A\textbf{v}_i \ne \textbf{0}$ if and only if $1\le i\le$. So $\left\{ A\textbf{v}_1 \cdots A\textbf{v}_n \right\}$ are linearly independent vectors, and they are in $\text{Col} A$. Finally, for any $\textbf{y}$ in $\text{Col} A$ —say,$\textbf{y}=A\textbf{x}$—we can write $\textbf{x} = c_1\textbf{v1}+\cdots+c_n\textbf{vn}$, and

$$\begin{align*} \textbf{y} &= A\textbf{x} \\ &= c_1 A \textbf{v}_1 +\cdots+ c_r A \textbf{v}_r + c_{r+1} A \textbf{v}_{r+1}+ \cdots +cn A \textbf{v}_n \\ &= c_1 A \textbf{v}_1 +\cdots+ c_r A \textbf{v}_r +\textbf{0}+\cdots+\textbf{0} \end{align*}$$

Thus $\textbf{y}$ is in Span $\left\{ A\textbf{v}_1 \cdots A\textbf{v}_n \right\}$, which shows that $\left\{ A\textbf{v}_1 \cdots A\textbf{v}_r \right\}$ is an (orthogonal) basis for $\text{Col} A$. Hence $\text{rank }A=dim \text{Col }A=r$. $\blacksquare$

Theorem 10: The Singular Value Decomposition

he decomposition of $A$ involves an $m \times n$ “diagonal” matrix $\Sigma$ of the form

$\tag{3}$

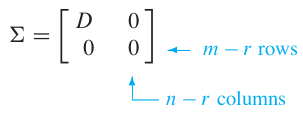
where $D$ is an $r \times r$ diagonal matrix for some $r$ not excedding the smaller of $m$ and $n$. (If $r$ equals $m$ or $n$ or both, some or all of the zero matrices do not appear.)

Let $A$ be an $m \times n$ matrix with rank $r$. Then there exists an $m \times n$ matrix $\Sigma$ as in (3) for which the diagonal entries in $D$ are the first $r$ singular values of $A$, $\sigma_1 \ge \sigma_2 \cdots, \sigma_r >0$, and there exists an $m \times m$ orthogonal matrix $U$ and an $n \times n$ orthogonal matrix $V$ such that $$A=U\Sigma V^T$$

Any factorization $A=U\Sigma V^T$, with $U$ and $V$ orthogonal, $\Sigma$ as in (3), and positive diagonal entries in $D$, is called a singular value decomposition (or SVD) of $A$.

The columns of $U$ in such a decomposition are called left singular vectors of $A$, and the columns of $V$ are called right singular vectors of $A$.

Proof of SVD

Let $\lambda_i$ and $\textbf{v}_i$ be as in Theorem 9, so that $\left\{ A\textbf{v}_1 \cdots A\textbf{v}_r \right\}$ is an orthogonal basis for $\text{Col }A$.

Normalize each $A\textbf{v}_i$ to obtain an orthonormal basis $\left\{ \textbf{u}_1 \cdots \textbf{u}_r \right\}$, where

$$\begin{align*} \textbf{u}_i &= \frac{1}{||A\textbf{v}_i||}A\textbf{v}_i \\ &= \frac{1}{\sigma_i}A\textbf{v}_i \end{align*}$$

And

$$A\textbf{v}_i = \sigma_i \textbf{u}_i \quad (1 \le i \le r) \tag{4}$$

Now extend $\left\{ \textbf{u}_1, \cdots, \textbf{u}_r\right\}$ to an orthonormal basis $\left\{ \textbf{u}_1, \cdots, \textbf{u}_m\right\}$ of $\mathbb{R}^m$, and let

$U = \begin{bmatrix} \textbf{u}_1 & \textbf{u}_2 & \cdots \textbf{u}_m \end{bmatrix}$ and $$V = \begin{bmatrix} \textbf{v}_1 & \textbf{v}_2 & \cdots \textbf{v}_n \end{bmatrix}$$

By construction, $U$ and $V$ are orthogonal matrices. Also, from (4),

$$\begin{align*} AV &= \begin{bmatrix} A\textbf{v}_1 & \cdots & A\textbf{v}_r & \textbf{0} & \textbf{0} \end{bmatrix} \\ &= \begin{bmatrix} \sigma_1\textbf{u}_1 & \cdots & \sigma_r\textbf{u}_r & \textbf{0} & \textbf{0} \end{bmatrix} \end{align*}$$

Let $D$ be the diagonal matrix with diagonal entries $\sigma_1 \cdots \sigma_r$, and let $\Sigma$ be as in (3) above. Then

![e1][./fig/la_07_04_e1.png]

Since $V$ is an orhtogonal matrix, $U\Sigma V^T = AV V^T = A$. $blacksquare$

The next two examples focus attention on the internal structure of a singular value decomposition. An efficient and numerically stable algorithm for this decomposition would use a different approach.