Ch05. Eigenvalues and Eigenvectors
5.4 Eigenvectors and Linear Transformations
The Matrix of a Linear Transformation
Given any in , the coordinate vector is in and the coordinate vector of its image, , is in , as shown in Fig. 1. below.
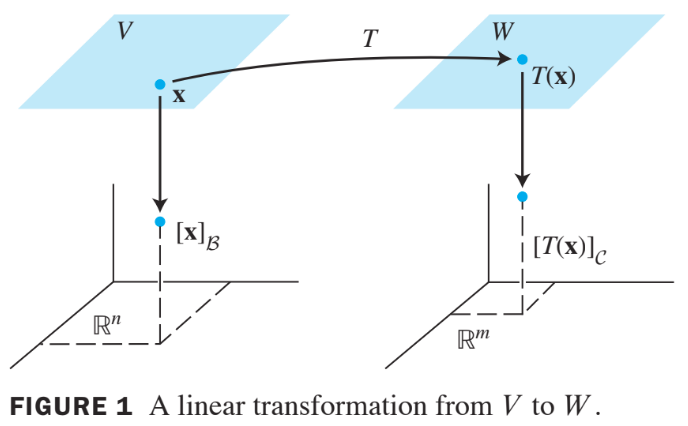
The connection between and is easy to find.
Let be the basis for. If then,
And because is linear.
Now, since the coordinate mapping from to is linear, equation (1) leads to
- Since -coordinate vectors are in , the vector equation (2) can be written as a matrix equation, namely, where
- The matrix is a matrix representation of , called the matrix for relative to the bases and . See Fig. 2 below:
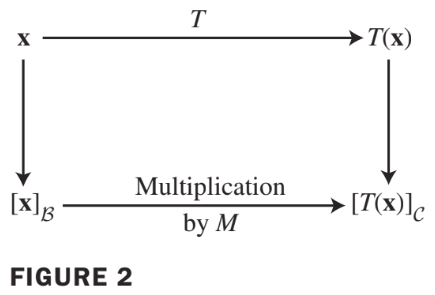
이 실제로 coordinate vector를 linear transform하여 목표로하는 basis의 coordinate vector로 mapping
Example 1
Suppose is a basis for and is a basis for . Let be a linear transformation with the property that
Find the matrix for relative to and .
Solution
The -coordinate vectors of the images of and are
- Hence
If and are bases for the same space and if is the identity transformation for , then Matrix in (4) is just a change-of-coordinates matrix.
4.7절 참고
Linear Transformations from V into V
- In the common case where is the same as and the basis is the same as , the matrix in (4) is called the matrix for relative to , or simply the -matrix for , and is denoted by .
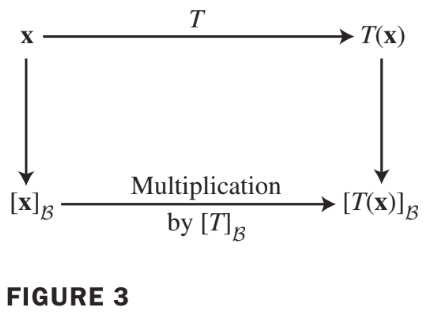
Example2
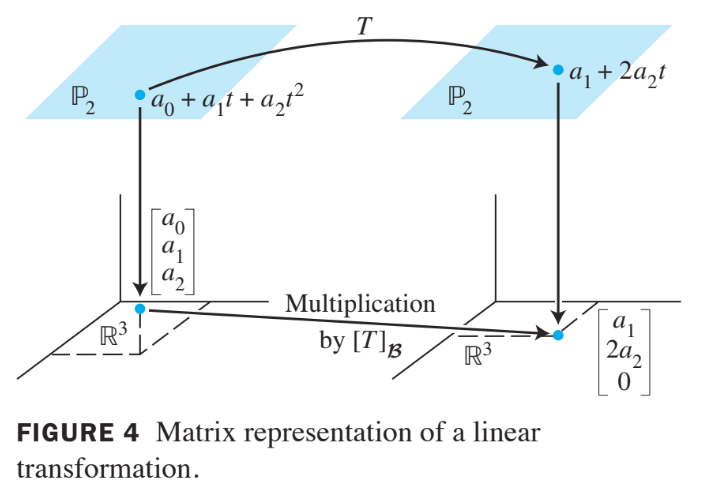
The mapping defined by is a linear transformation.
- Find the -matrix for , when is the basis
- Verify that
Solution
Compute the images of the basis vectors:
Then write the -coordinate vector of , and and place them together as the -matrix for :
For a general ,
- SeeFig. 4 below
Linear Transformations on R to the n Power
A가 대각화가 가능한 경우, 의 eigenvector들로 구성된 basis 이 존재하며, Linear Transform 에 대한 -matrix for 는 diagonal matrix임. 아래의 Theorem 8은 이 사실을 보여줌.
Theorem 8:
Suppose where is a diagonal matrix. If is the basis for formed from the columns of , then is the -matrix for the transformation .
Proof
Denote the columns of by , so that and . In this case, is the change-of-coordinates matrix discussed in Section 4.4, where
If for , then
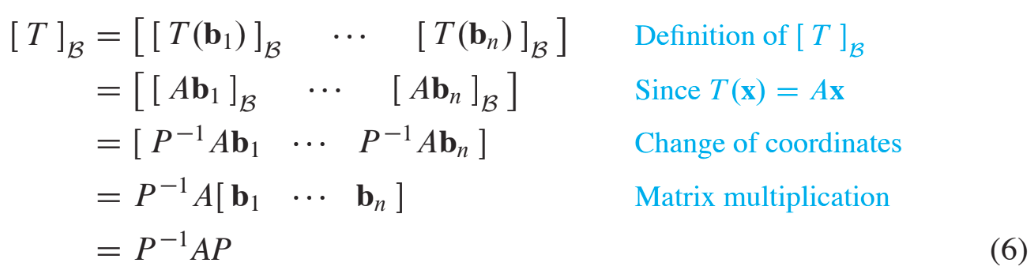
Since , we have .
Example3
Define by , where . Find a basis for with the property that the -matrix for is a diagonal matrix.
Solution
From Example 2 in section 5.3 we know that , where
- The columns of , call them and , are eigenvectors of . By Theorem 8, is the -matrix for when . The mappings and describe the same linear transformation, relative to different bases.