Ch05. Eigenvectors and Eigenvalues

5.1 Eigenvectors and Eigenvalues

We will study special vectors which are transformed by $A$ into scalar multiples of themselves.

Definition

• An eigenvector of an $n \times n$ matrix $A$ is a nonzero vector $\textbf{x}$ such that $A\textbf{x}=\lambda \textbf{x}$ for some scalar $\lambda$.
• A scalar $\lambda$ is called an eigenvalue of $A$ if there is a nontrivial solution $\textbf{x}$ of $A\textbf{x}=\lambda \textbf{x}$; such an $\textbf{x}$ is called an eigenvector corresponding to $\lambda$.

$\lambda$ is an eigenvalue of an $n \times n$ matrix $A$ if and only if the equation $$(A-\lambda I)\textbf{x}=\textbf{0} \tag{3}$$ has a nontrivial solution ($\textbf{x} \ne \textbf{0}$).

• The set of all solutions of (3) is just the null space of the matrix $A-\lambda I$.
• So this set is
  • a subspace of $\mathbb{R}^n$ and
  • is called the eigenspace of $A$ corresponding to $\lambda$.
• The eigenspace consists of the zero vector and all the eigenvectors corresponding to $\lambda$.

• Eigen vector
• Eigen value
• Eigen space!

Example 3

Show that 7 is an eigenvalue of matrix $A=\begin{bmatrix} 1 & 6 \\ 5 & 2 \end{bmatrix}$ and find the corresponding eigenveoctors.

Solution:

The scalar 7 is an eigenvalue of $A$ if and only if the equation $$A\textbf{x}=7\textbf{x} \tag{1}$$ has a nontrivial solution.

• But (1) is equivalent to $A\textbf{x}-7\textbf{x}=\textbf{0}$, or $$(A-7I)\textbf{x}=\textbf{0} \tag{2}$$
• To solve this homogeneous equation, form the matrix $$(A-7I)=\begin{bmatrix} 1 & 6 \\ 5 & 2 \end{bmatrix} - \begin{bmatrix} 7 & 0 \\ 0 & 7 \end{bmatrix} = \begin{bmatrix} -6 & 6 \\ 5 & -5 \end{bmatrix}$$
• The columns of $(A-7I)$ are obviously linearly dependent, so (2) has nontrivial solutions.

To find the corresponding eigenvectors, use row operations: $$\begin{bmatrix} -6 & 6 & 0\\ 5 & -5 & 0\end{bmatrix} \sim \begin{bmatrix} 1 & -1 & 0\\ 0 & 0 & 0\end{bmatrix}$$

• The general solution has the form $x_2 \begin{bmatrix} 1 \\ 1 \end{bmatrix}$.
• Each vector of this form with $x_2 \ne 0$ is an eigenvector corresponding to $\lambda=7$.

Example 4

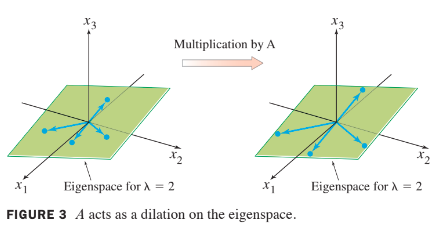
Let $A=\begin{bmatrix}4&-1&6\\2&1&6\\2&-1&8\end{bmatrix}$. An eigenvalue of $A$ is 2. Find a basis for the corresponding eigenspace.

Solution:

Form $$A-2I = \begin{bmatrix}4&-1&6\\2&1&6\\2&-1&8\end{bmatrix} -\begin{bmatrix}2&0&0\\0&2&0\\0&0&2\end{bmatrix} =\begin{bmatrix}2&-1&6\\2&-1&6\\2&-1&6\end{bmatrix}$$ and row reduce the augmented matrix for $(A-2I)\textbf{x}=\textbf{0}$. $$\begin{bmatrix}2&-1&6&0\\2&-1&6&0\\2&-1&6&0\end{bmatrix} \sim \begin{bmatrix}2&-1&6&0\\0&0&0&0\\0&0&0&0\end{bmatrix}$$

• At this point, it is clear that 2 is indeed an eigenvalue of $A$ because the equation $(A-2I)\textbf{x}=\textbf{0}$ has free variables.
• The general solution is $\begin{bmatrix}x_1 \\ x_2 \\ x_3 \end{bmatrix} = x_2 \begin{bmatrix} \frac{1}{2} \\1 \\0 \end{bmatrix} +x_3 \begin{bmatrix} -3 \\ 0 \\ 1 \end{bmatrix}$, $x_2, \text{ and } x_3$ free.

The eigenspace, shown in the following figure, is a two-dimensional subspace of $\mathbb{R}^3$. A basis is $$\left \{ \left[\begin{matrix} 1 \\ 2\\ 0 \end{matrix}\right] , \left[\begin{matrix} -3 \\ 0\\ 1 \end{matrix}\right] \right \}$$

Example 4 shows a good method for manual computation of eigenvectors in simple cases when an eigenvalue is known. Using a matrix program and row reduction to find an eigenspace (for a specified eigenvalue) usually works, too, but this is not entirely reliable. Roundoff error can lead occasionally to a reduced echelon form with the wrong number of pivots. The best computer programs compute approximations for eigenvalues and eigenvectors simultaneously, to any desired degree of accuracy, for matrices that are not too large. The size of matrices that can be analyzed increases each year as computing power and software improve.

The following theorem describes one of the few special cases in which eigenvalues can be found precisely.

Theorem 1

The eigenvalues of a triangular matrix are the entries on its main diagonal.

Proof

For simplicity, consider the $3 \times 3$ case.

• If $A$ is upper tirangular, the $A-\lambda I$ ahs the form $$\begin {align} A-\lambda I & = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{bmatrix} - \begin{bmatrix} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \end{bmatrix} \\ &= \begin{bmatrix} a_{11} - \lambda & a_{12} & a_{13} \\ 0 & a_{22}- \lambda & a_{23} \\ 0 & 0 & a_{33}- \lambda \end{bmatrix} \end {align}$$
• The scalar $\lambda$ is an eigenvalue of $A$ if and only if the equation $(A-\lambda I)\textbf{x}=\textbf{0}$ has a nontrivial solution, that is, if and only if the equation has a free variable.
• Because of the zero entries in $A-\lambda I$, it is easy to see that $(A-\lambda I)\textbf{x}=\textbf{0}$ has a free variable if and only if at least one of the entries on the diagonal of $A-\lambda I$ is zero.
• This happens if and only if $\lambda$ equals one of the entries $a_{11}, a_{22}, a_{33}$ in $A$.

Theorem 2

If $\textbf{v}_1,\cdots,\textbf{v}_r$ are eigenvectors that correspond to distinct eigenvalues $\lambda_1, \cdots \lambda_r$ of an $n \times n$ matrix $A$, then the set $\left\{\textbf{v}_1,\cdots,\textbf{v}_r\right\}$ is linearly independent.

Proof

Suppose $\left\{\textbf{v}_1,\cdots,\textbf{v}_r\right\}$ is linearly dependent.

• Since $\textbf{v}_1$ is nonzero, Theorem 7 in Section 1.7 says that one of the vectors in the set is a linear combination of the preceding vectors.
• Let $p$ be the least index such that $\textbf{v}_{p+1}$ is a linear combination of the preceding (linearly independent) vectors.
• Then there exist scalars $c_1 \cdots c_p$ such that $$c_1 \textbf{v}_1 + \cdots + c_p \textbf{v}_p = \textbf{v}_{p+1} \tag{5}$$
• Multiplying both sides of (5) by $A$ and using the fact that $A\textbf{v}_k = \lambda_k\textbf{v}_k$ for each $k$, we obtain $$c_1 A \textbf{v}_1 + \cdots + c_p A \textbf{v}_p = A \textbf{v}_{p+1} \\ c_1 \lambda_1 \textbf{v}_1 + \cdots + c_p \lambda_p \textbf{v}_p = \lambda_{p+1} \textbf{v}_{p+1} \tag{6}$$
• Multiplying both sides of (5) by $\lambda_{p+1}$ and subtracting the result from (6), we have $$c_1 (\lambda_1-\lambda_{p+1}) \textbf{v}_1 + \cdots + c_p (\lambda_p-\lambda_{p+1}) \textbf{v}_p = \textbf{0} \tag{7}$$
• Since $\left\{\textbf{v}_1,\cdots,\textbf{v}_p\right\}$ is linearly independent, the weidhts in (7) are all zero.
• But none of the factors $\lambda_i-\lambda_{p+1}$ are zero, because the eigenvalues are distinct.
• Hence $c_i=0$ for $i=1,\cdots,p$.
• But then (5) says that $\textbf{v}_{p+1}=\textbf{0}$, which is impossible.
• Hence $\left\{\textbf{v}_1,\cdots,\textbf{v}_p\right\}$ cannot be linearly dependent and therefore must be linearly independent.

Eigenvectors and Difference Equations

There is a difference equation

$$\textbf{x}_{k+1} = A \textbf{x}_k \tag{8}$$

• If $A$ is an $n \times n$ matrix, then (8) is a recursive description of a sequence $\left\{ \textbf{x}_k\right\}$ in $\mathbb{R}^n$.
• A solution of (8) is an explicit description of $\left\{ \textbf{x}_k\right\}$ whose formula for each $\textbf{x}_k$ does not depend directly on $A$ or on the preceding terms in the sequence other than the initial term $\textbf{x}_0$.
• The simplest way to build a solution of (8) is to take an eigenvector $\textbf{x}_0$ and its corresponding eigenvalue $\lambda$ and let $$\textbf{x}_k = \lambda^k\textbf{x}_0 (k=1,2,\cdots) \tag{9}$$
• This sequence is a solution because $$A\textbf{x}_k = A (\lambda^k \textbf{x}_0) = \lambda^k (A \textbf{x}_0) = \lambda^k (\lambda \textbf{x}_0) = \lambda^{k+1}\textbf{x}_0 = \textbf{x}_{k+1}$$