Ch02. Matrix Algebra

2.5 Matrix Factorizations

Matrix Factorizations

• A Factorization of a matrix $A$ is an equation that expresses $A$ as a product of two or more matrices.
• Whereas matrix multiplication involves a synthesis of data (combining the effects of two or more linear transformations into a single matrix), matrix factorization is an analysis of data.

The LU Factorization

The LU Factorization is motivated by the fairly common industrial and business problem of solving a sequence of equations, all with the same coefficient matrix:

$$A\textbf{x}=\textbf{b}_1,A\textbf{x}=\textbf{b}_2, \cdots, A\textbf{x}=\textbf{b}_p \tag{1}$$

• When $A$ is invertible, one could compute $A^{-1}$ and then compute $A^{-1}\textbf{b}_1, A^{-1}\textbf{b}_2$ and so on. However, it is more efficient to solve the first equation in the sequence (1) by row reduction and LU factorization of $A$ at the same time. Thereafter the remaining equations in sequence(1) are solved with the LU factorization.
• At first, assume that $A$ is an $m \times n$ matrix that can be row reduction to echelon form, without row interchanges.
• Then $A$ can be written in the form $A=LU$, where $L$ is an $m\times m$ lower triangular matrix with 1's on the diagonal and $U$ is an $m \times n$ echelon form of $A$.
• For instance, see Fig. 1 below. Such a factorizaton is called an LU factorization of $A$. The matrix $L$ is invertible and is called a unit lower triangular matrix.

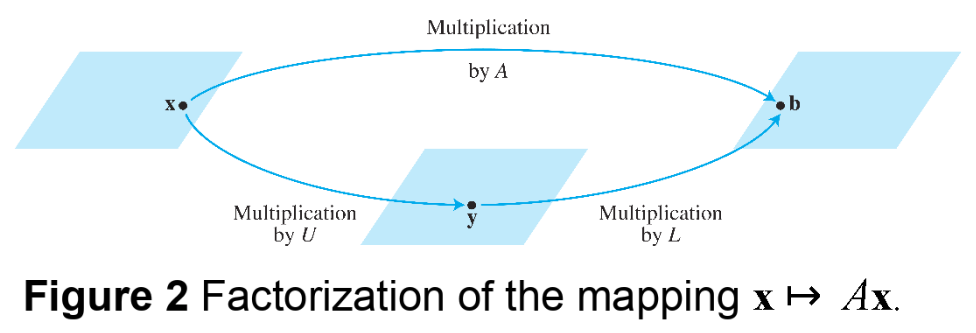
• Before studying how to construct $L$ and $U$, we should look at why they are so useful. When $A=LU$, the equation $A\textbf{x}=\textbf{b}$ can be written as $L(U\textbf{x})=\textbf{b}$.
• Writing $\textbf{y}$ for $U\textbf{x}$, we can find $\textbf{x}$ by solving the pair of equations

$$L\textbf{y}=\textbf{b} \\ U\textbf{x}=\textbf{y} \tag{2}$$ $$A=\begin{bmatrix} 1 & 0 & 0 & 0 \\ * & 1 & 0 & 0 \\ * & * & 1 & 0 \\ * & * & * & 1 \end{bmatrix} \begin{bmatrix} \blacksquare & * & * & * & * \\ 0 & \blacksquare & * & * & * \\ 0 & 0 & 0 & \blacksquare & * \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}$$

• First solve $L\textbf{y}=\textbf{b}$ for $\textbf{y}$, and then
• solve $U\textbf{x}=\textbf{y}$ for $\textbf{x}$.

See Fig 2. Each equation is easy to solve because $L$ and $U$ are triangular.

Example 1

It can be verified that

$$A=\begin{bmatrix} 3 & -7 & -2 & 2 \\ -3 & 5 & 1 & 0 \\ 6 & -4 & 0 &-5 \\ -9 & 5 & -5 & 12 \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 & 0 \\ -1 & 1 & 0 & 0 \\ 2 & -5 & 1 & 0 \\ -3 & 8 & 3 & 1 \end{bmatrix} \begin{bmatrix} 3 & -7 & -2 & 2 \\ 0 & -2 & -1 & 2 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & 0 & -1 \end{bmatrix} =LU$$

Use this factorization of $A$ to solve $A\textbf{x}=\textbf{b}$, where $$\textbf{b}=\begin{bmatrix}-9 \\ 5\\ 7 \\ 11 \end{bmatrix}$$ .

Solution :

The solution of $L\textbf{y}=\textbf{b}$ needs only 6 multiplications and 6 additions, because the arithmetic takes place only in column 5.

$$\begin{bmatrix} L & \textbf{b} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & -9 \\ -1 & 1 & 0 & 0 & 5 \\ 2 & -5 & 1 & 0 & 7 \\ -3 & 8 & 3 & 1 & 11 \end{bmatrix} \sim \begin{bmatrix} 1 & 0 & 0 & 0 & -9 \\ 0 & 1 & 0 & 0 & -4 \\ 0 & 0 & 1 & 0 & 5 \\ 0 & 0 & 0 & 1 & 1 \end{bmatrix} = \begin{bmatrix} I & \textbf{y} \end{bmatrix}$$

• Then, for $U \textbf{x}=\textbf{y}$, the "backward" phase of row reduction requires 4 divisions, 6 multiplications, and 6 additions.
• For instance, creating the zeros in column 4 of $\begin{bmatrix} U & \textbf{y} \end{bmatrix}$ requires 1 division in row 4 and 3 multiplication-addition pairs to add multiples of row 4 to the rows above.

$$\begin{bmatrix} U & \textbf{y} \end{bmatrix} = \begin{bmatrix} 3 & -7 & -2 & 2 & -9 \\ 0 & -2 & -1 & 2 & -4 \\ 0 & 0 & -1 & 1 & 5 \\ 0 & 0 & 0 & -1 & 1 \end{bmatrix} \sim \begin{bmatrix} 1 & 0 & 0 & 0 & 3 \\ 0 & 1 & 0 & 0 & 4 \\ 0 & 0 & 1 & 0 & -6 \\ 0 & 0 & 0 & 1 & -1 \end{bmatrix}, \textbf{x}= \begin{bmatrix} 3 \\ 4\\-6 \\ -1 \end{bmatrix}$$

• To find $\textbf{x}$ requires 28 arithmetic operations, or "flops"(floating point operations), excluding the cost of finding $L$ and $U$. In contrast, row reduction of $\begin{bmatrix} A & \textbf{b} \end{bmatrix}$ to $\begin{bmatrix} I \textbf{x} \end{bmatrix}$ takes 62 operations.

An LU Factorization Algorithm

• Suppose $A$ can be reduced to an echelon form $U$ using only row replacements that add a multiple of one row to another below it. (interchange없이 U로 축소시킴.)
• In this case, there exist unit lower triangular elementary matrices $E_1 \cdots E_p$ such that

$$E_p \cdots E_1 A = U \tag{3}$$

• Then

$$A = (E_p \cdots E_1 )^{-1}U = LU$$

• where

$$L = (E_p \cdots E_1) ^{-1} \tag{4}$$

• It can be shown that products and inverses of unit lower triangular matrices are also unit lower triangular. Thus $L$ is unit lower triangular.
• Note that row operations in equation (3), which reduce $A$ to $U$, also reduce the $L$ in equation (4) to $I$, because $E_p \cdots E_1 L = (E_p \cdots E_1)(E_p \cdots E_1)^{-1}=I$. This observation is the key to constructing $L$.

Algorithm for an L U Factorization

1. Reduce $A$ to an echelon form $U$ by a sequence of row replacement operations, if possible.
2. Place entries in $L$ such that the same sequence of row operations reduces $L$ to $I$.

• Step 1 is not always possible, but when it is, the argument above shows that an $L U$ factorization exists.

  square matrix이면서 interchange없이 row reduction을 수행하여 echelon form이 될 수 있는 경우에는 반드시 LU Factorization이 가능함 (충분조건으로, 역은 성립하지 않음.).

  즉, interchage를 해야만 row echelon form이 되더라도 LU Factorization이 되는 경우도 존재함. $A=\begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 3 & 0 & 0 \end{bmatrix}=\begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 3 & 0 & 0 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}= LU$

• Example 2 will show how to implement step 2. By construction, $L$ will satisfy $(E_p\cdots E_1)L = I$ using the same $E_p, \cdots E_1$ as in equation (3). Thus $L$ will be invertible, by the invertible matrix theorem, with $(E_p \cdots E_1 ) = L^{-1}$. From (3), $L^{-1} A = U$, and $A = LU$. So step 2 will produce an acceptable $L$.

Example 2

Find an $LU$ factorization of

$$A =\begin{bmatrix} 2 & 4 & -1 & 5 & -2 \\ -4 & -5 & 3 & -8 & 1 \\ 2 & -5 & -4 & 1 & 8 \\ -6 & 0 & 7 & -3 & 1 \end{bmatrix}$$

Solution :

Since $A$ has four rows, $L$ should be $4 \times 4$. The first column of $L$ is the first column of $A$ divided by the top pivot entry:

$$L =\begin{bmatrix} 1 & 0 & 0 & 0 \\ -2 & 1 & 0 & 0 \\ 1 & & 1 & 0 \\ -3 & & & 1 \end{bmatrix}$$

• Compare the first columns of $A$ and $L$. The row operations that create zeros in the first column of $A$ will also create zeros in the first column of $L$.

• To make this same correspondence of row operations on $A$ hold for the rest of $L$, watch a row reduction of $A$ to an echelon form $U$. That is, highlight the entries in each matrix that are used to determine the sequence of row operations that transform $A$ onto $U$.

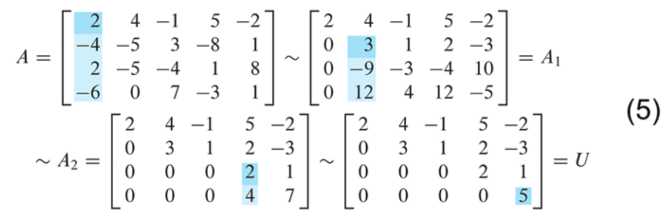
The highlighted entries above determine the row reduction of $A$ to $U$. At each pivot column, divide the highlighted entries by the pivot and place the result onto $L$:

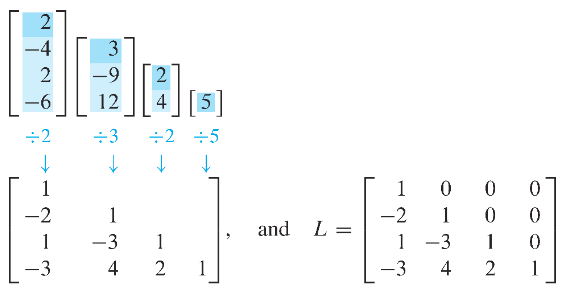
• An easy calculation verifies that this $L$ and $U$ satisfy $LU=A$ $\blacksquare$

A 가 invertible 이면서 LU factorizatoin이 가능할 경우, U(A의 row echelon form)의 diagonal entries는 모두 1이 될 수 있으며, L의 diagonal entries에는 0이 존재 하지 않음(L이 triangular matrix이면서 invertible이기 때문임.). L도 모든 diagonal entries를 1로 만들기 위해서는 LU factorization을 조금 변형하여 LDU factorization으로 처리하면 됨. LDU의 경우, L과 U가 LU factorization과 달리 유일하게 결정됨(물론 D도 유일).