Linear Equations in Linear Algebra

1.7 Linear Independence

Linear Independence

Definition : Linear Independence

An indexed set of vectors $\left\{ \textbf{v}_1, \textbf{v}_2, \cdots,\textbf{v}_p \right\}$ in $\mathbb{R}^n$ is said to be linearly independent if the vector equation

$$x_1 \textbf{v}_1+x_2 \textbf{v}_2+ \cdots +x_p \textbf{v}_p = \textbf{0} \tag{1}$$

has only the trivial solution (=only zero vector can be $\textbf{x}$).

That is, the set $\left\{\textbf{v}_1, \textbf{v}_2, \cdots,\textbf{v}_p \right\}$ is said to be linearly dependent if there exist weights $c_1,\cdots,c_p$, not all zero, such that $$c_1\textbf{v}_1 +c_2\textbf{v}_2 +\cdots+c_p\textbf{v}_p = \textbf{0} \tag{2}$$

$$\blacksquare$$

• Equation (2) is called a linear dependence relation among $\left\{\textbf{v}_1, \textbf{v}_2, \cdots,\textbf{v}_p \right\}$ when the weights are not all zero.
• An indexed set is linearly dependent if and only if it is not linearly independent.

Practical Definition : Linear Independence

Given a set of vectors $\left \{\textbf{v}_1, \textbf{v}_2, \cdots,\textbf{v}_p \right\}$ in $\mathbb{R}^n$,

check if $\textbf{v}_j$ can be represented as a linear combination of the previous vectors of the set $\left\{\textbf{v}_1, \textbf{v}_2, \cdots,\textbf{v}_p \right\}$ for $j=1,\cdots, p$, e.g., $\textbf{v}_j \in \text{Span} \left\{ \textbf{v}_1, \textbf{v}_2, \cdots,\textbf{v}_{j-1} \right\} \text{ for some }j=1,\cdots,p \text{?}$

• If at least one such $\textbf{v}_j$ is found, then $\left\{\textbf{v}_1, \textbf{v}_2, \cdots,\textbf{v}_p \right\}$ is linearly dependent.
• If no such $\textbf{v}_j$ is found, then $\left\{\textbf{v}_1, \textbf{v}_2, \cdots,\textbf{v}_p \right\}$ is linearly independent.

Example 1

Let $\textbf{v}_1=\begin{bmatrix} 1 \\ 2\\ 3 \end{bmatrix}, \textbf{v}_2=\begin{bmatrix} 4 \\ 5\\ 6 \end{bmatrix}$, and $\textbf{v}_1=\begin{bmatrix} 2 \\ 1\\ 0 \end{bmatrix}$.

1. Determine if the set $\left\{\textbf{v}_1, \textbf{v}_2, \textbf{v}_3 \right\}$ is linearly independent.
2. If possible, find a linear dependence relation among $\textbf{v}_1$, $\textbf{v}_2$, and $\textbf{v}_3$.

Solution of Example 1:

1.

We must determine if there is a nontrivial solution of the equation (1).

• Row operations on the associated augmented matrix show that $\begin{bmatrix}1 & 4& 2& 0\\2 &5&1&0 \\ 3&6&0 &0 \end{bmatrix} \text{~} \begin{bmatrix}1 & 4& 2& 0\\0 &-3&-3&0\\ 0&0&0 &0 \end{bmatrix}$
• $x_1$ and $x_2$ are basic variables, and $x_3$ is free.
• Each nonzero value of $x_3$ determines a nontrivial solution.
• $\textbf{v}_1$, $\textbf{v}_2$, $\textbf{v}_3$ are linearly dependent.

2.

To find a linear dependence relation among $\textbf{v}_1$, $\textbf{v}_2$, and $\textbf{v}_3$ completely row reduce the augmented matrix and write the new system:

$$\begin{bmatrix}1 & 0& -2& 0\\ 0 &1&1&0 \\ 0&0&0 &0 \end{bmatrix} \begin{align}x_1 -2x_3 &=0 \\ x_2+x_3 &=0 \\0 &= 0\end{align}$$

• Thus $x_1=2x_3$ and $x_2=-x_3$ and $x_3$ is free.
• Choose nonzero value for $x_3$, e.g., $x_3=5$.
• Then $x_1=10$ and $x_2=-5$.
• Substitute these values into equation (1) and obtain the equation below. $10 \textbf{v}_1-5 \textbf{v}_2+ 5 \textbf{v}_3 = 0$
• This is one (out of infinitely many) possible linear dependence relations among $\textbf{v}_1$, $\textbf{v}_2$, and $\textbf{v}_3$. $\blacksquare$

Linear Independence of Matrix Columns

Suppose that we begin with a matrix $A=\begin{bmatrix} \textbf{a}_1 & \cdots &\textbf{a}_n \end{bmatrix}$ instead of a set of vectors.

The matrix equation $A\textbf{x}=\textbf{0}$ can be written as $x_1\textbf{a}_1+ x_2\textbf{a}_2+ \cdots+x_n\textbf{a}_n = \textbf{0}$

Each linear dependence relation among the columns of $A$ corresponds to a nontrivial solution of $A\textbf{x}=\textbf{0}$

The columns of matrix $A$ are linearly independent if and only if the equation $A\textbf{x}=\textbf{0}$ has only the trivial solution.

$\blacksquare$

Sets of One or Two Vectors

A set containing only one vector – say, $\textbf{v}$ – is linearly independent if and only if $\textbf{v}$ is not the zero vector.

• This is because the vector equation $x_1\textbf{v}=\textbf{0}$ has only the trivial solution when $\textbf{v} \ne \textbf{0}$.

• The zero vector is linearly dependent because $x_1\textbf{0}=\textbf{0}$ has many nontrivial solutions.

• A set of two vectors $\left\{\textbf{v}_1, \textbf{v}_2 \right\}$ is linearly dependent if at least one of the vectors is a multiple of the other.

The set is linearly independent if and only if neither of the vectors is a multiple of the other.

$\blacksquare$

Sets of Two or More Vectors

Theorem 7 : Characterization of Linearly Dependent Sets

An indexed set $S=\left\{\textbf{v}_1, \textbf{v}_2, \cdots,\textbf{v}_p \right\}$ of two or more vectors is linearly dependent if and only if at least one of the vectors in $S$ is a linear combination of the others. In fact, if $S$ is linearly dependent and $\textbf{v}_1 \ne \textbf{0}$ then some $\textbf{v}_j$ (with $j>1$) is a linear combination of the preceding vectors, $\textbf{v}_1, \textbf{v}_2, \cdots,\textbf{v}_{j-1}$.

• Theorem 7 does not say that every vector in a linearly dependent set is a linear combination of the preceding vectors.

• A vector in a linearly dependent set may fail to be a linear combination of the other vectors.

Proof of Theorem 7:

• If some $\textbf{v}_j$ in $S$ equals a linear combination of the other vectors,then $\textbf{v}_j$ can be subtracted from both sides of the equation, producing a linear dependence relation with a nonzero weight (−1) on $\textbf{v}_j$

• e.g., if $\textbf{v}_1=c_2 \textbf{v}_2 +c_3 \textbf{v}_3$, then $\textbf{0} = -\textbf{v}_1 + c_2 \textbf{v}_2 +c_3 \textbf{v}_3 + 0 \textbf{v}_4 +\cdots+0\textbf{v}_p$.

• Thus $S$ is linearly dependent.

• Conversely, suppose $S$ is linearly dependent.

• If $\textbf{v}_1$ is zero, then it is a (trivial) linear combination of the other vectors in $S$.

  즉, zero vector를 포함한 경우, 해당 집합은 항상 linearly dependent가 된다. zero vector의 coef.는 무엇이든지간에 0이 되기 때문임.

• Otherwise, $\textbf{v}_1 \ne \textbf{0}$ and there exist weights $c_1,\cdots,c_p$, not all zero, such that $c_1\textbf{v}_1 +c_2\textbf{v}_2 +\cdots +c_p\textbf{v}_p =\textbf{0}$.

• Let $j$ be the largest subscript for which $c_j \ne 0$.

• If $j=1$ then $c_1\textbf{v}_1 = \textbf{0}$, which is impossible because $\textbf{v}_1 \ne \textbf{0}$.

  ($j=1$인 경우, 1보다 큰 $c_j$들은 모두 0이되어야 함. 즉, 나머지 coef들은 모조리 0이므로 남는 건 $c_1\textbf{v}_1$항 뿐으로 $c_1\textbf{v}_1=0$가 되어야 하는데 이는 불가능함.)

• So $j>1$

• And $$\begin{align} c_1\textbf{v}_1 +\cdots+c_j\textbf{v}_j +0\textbf{v}_{j+1} + \cdots + 0\textbf{v}_p &=\textbf{0}\\ c_j\textbf{v}_j &= -c_1\textbf{v}_1 -\cdots -c_{j-1}\textbf{v}_{j-1} \\ v_j &= \left(-\frac{c_1}{c_j}\right)\textbf{v}_1+\cdots+\left(-\frac{c_{j-1}}{c_j}\right)\textbf{v}_{j-1} \end{align}\\ \blacksquare$$

Example 4

Let $\textbf{u}=\begin{bmatrix} 3 \\ 1\\ 0\end{bmatrix}$ and $\textbf{v}=\begin{bmatrix} 1 \\ 6\\ 0\end{bmatrix}$.

Describe the set spanned by $\textbf{u}$ and $\textbf{v}$, and explain why a vector $\textbf{w}$ is in Span $\left\{\textbf{u}, \textbf{v} \right\}$ if and only if $\left\{ \textbf{u},\textbf{v}, \textbf{w} \right\}$ is linearly dependent.

Solution of Example 4:

• The vectors $\textbf{u}$ and $\textbf{v}$ are linearly independent because neither vector is a multiple of the other, and so they span a plane in $\mathbb{R}^3$.

• Span $\left\{\textbf{u}, \textbf{v}\right\}$ is the $x_1x_2$-plane with $x_3=0$.

• If $\textbf{w}$ is a linear combination of $\textbf{u}$ and $\textbf{v}$, then $\left\{\textbf{u}, \textbf{v},\textbf{w}\right\}$ is linearly dependent, by Theorem 7.

• Conversely, suppose that $\left\{\textbf{u}, \textbf{v},\textbf{w}\right\}$ is linearly dependent.

• By Theorem 7, some vector in $\left\{\textbf{u}, \textbf{v},\textbf{w}\right\}$ is a linear combination of the preceding vectors since $\textbf{u} \ne \textbf{0}$.

• That vector must be $\textbf{w}$, since $\textbf{v}$ is not a multiple of $\textbf{u}$.

• So $\textbf{w}$ is in Span $\left\{\textbf{u}, \textbf{v}\right\}$. Fig.2 below

$\blacksquare$

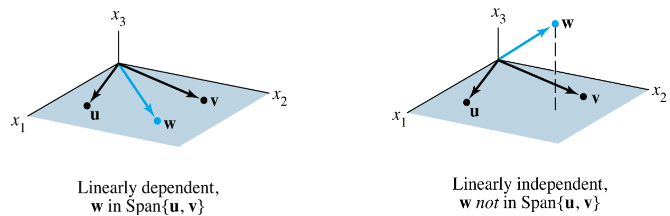
• Example 4 generalizes to any set $\left\{\textbf{u}, \textbf{v},\textbf{w}\right\}$ in $\mathbb{R}^3$ with $\textbf{u}$ and $\textbf{v}$ linearly independent.

• The set $\left\{\textbf{u}, \textbf{v},\textbf{w}\right\}$ will be linearly dependent if and only if $\textbf{w}$ is in the plane spanned by $\textbf{u}$ and $\textbf{v}$.

Theorem 8

If a set contains more vectors than there are entries in each vector, then the set is linearly dependent. That is, any set $\left\{ \textbf{v}_1, \cdots, \textbf{v}_p \right\} \in \mathbb{R}^n$ is linearly dependent if $p>n$.

Proof

• Let $A=\left\{ \textbf{v}_1, \cdots, \textbf{v}_p \right\}$.

• Then $A$ is $n\times p$, and the equation $A\textbf{x}=\textbf{0}$ corresponds to a system of $n$ equation in $p$ unknowns.

• If $p>n$, there are more variables than equations, so there must be a free variable.

• Hence $A\textbf{x}=\textbf{0}$ has a nontrivial solution, and the columns of $A$ is linearly dependent.

• See the figure below for a matrix version of this theorem.

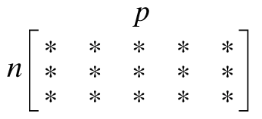
• if $p>n$, the columns are linearly dependent. $\blacksquare$

• Theorem 8 says nothing about the case in which the number of vectors in the set does not exceed the number of entries in each vector.

Theorem 9

If a set $S=\left\{ \textbf{v}_1, \cdots, \textbf{v}_p \right\} \in \mathbb{R}^n$ contains the zero vector, then the set is linearly dependent.

Proof of Theorem 9

• By renumbering the vectors, we may suppose $\textbf{v}_1 = \textbf{0}$.

• Then the equation $1\textbf{v}_1+0\textbf{v}_2+\cdots+0\textbf{v}_p=\textbf{0}$ shows that $S$ is linearly dependent. $\blacksquare$