Ch04 Vector Spaces

4.2 Null Spaces, Column Spaces, and Linear Transformations

Definition : Null Space

The null space of an $m \times n$ matrix $A$, written as Nul $A$, is the set of all solutions of the homogeneous equation $A\textbf{x}=\textbf{0}$. In set notation,

$$\text{Nul }A = \left\{ \textbf{x}:\textbf{x} \text{ is in }\mathbb{R}^n \text{ and } A\textbf{x}=\textbf{0} \right\}.$$

Theorem 2

The null space of an $m \times n$ matrix $A$ is a subspace of $\mathbb{R}^n$. Equivalently, the set of all solutions to a system $A\textbf{x}=\textbf{0}$ of $m$ homogeneous linear equations in $n$ unknowns is a subspace of $\mathbb{R}^n$.

Proof

• Nul $A$ is a subset of $\mathbb{R}^n$ because $A$ has $n$ columns.
• We need to show that Nul $A$ satisfies the three properties of a subspace.
• $\textbf{0}$ is in Nul $A$.
• Next, let $\bf{u}$ and $\bf{v}$ represent any two vectors in Nul $A$.
• Then

$$A\textbf{u}=\textbf{0} \text{ and } A\textbf{v}=\textbf{0}$$

• To show that $\textbf{u} + \textbf{v}$ is in Nul $A$, we must show that $A(\textbf{u}+\textbf{v})=\textbf{0}$.
• Using a property of matrix multiplication, compute

$$A(\textbf{u}+\textbf{v})= A\textbf{u} + A\textbf{v} = \textbf{0}+\textbf{0} = \textbf{0}$$

• Thus $\textbf{u}+\textbf{v}$ is in Nul $A$, and Nul $A$ is closed under vector addition.
• Finally, if $c$ is any scalar, then $$A(c\textbf{u}) = c(A\textbf{u}) = c(\textbf{0}) = \textbf{0}$$ which shows that $c\textbf{u}$ is in Nul $A$.

An Explicit Description of Nul A

• There is no obvious relation between vectors in Nul $A$ and the entries in $A$.
• We say that Nul $A$ is defined implicitly, because it is defined by a condition that must be checked.
• No explicit list or description of the elements in Nul $A$ is given.
• Solving the equation $A\textbf{x}=\textbf{0}$ amounts to producing an explicit description of Nul $A$.

Example 3:

Find a spanning set for the null space of the matrix

$$\left[ \begin{matrix} -3 & 6 & -1 & 1 & -7\\ 1 & -2 & 2 & 3 & -1 \\ 2 & -4 & 5 & 8 & -4 \end{matrix} \right]$$

Solution:

• The first step is to find the general solution of $A\textbf{x}=\textbf{0}$ in terms of free variables.
• Row reduce the augmented matrix $\begin{bmatrix} A & \textbf{0}\end{bmatrix}$ to reduce echelon form in order to write the basic variables in terms of the free variables:

$$\displaystyle \begin{matrix} \left[ \begin{matrix} -3 & 6 & -1 & 1 & -7 & 0\\ 1 & -2 & 2 & 3 & -1 & 0\\ 2 & -4 & 5 & 8 & -4 & 0 \end{matrix} \right] & \begin{align} x_1-2x_2-x_4+3x_5 &=0\\ x_3+2x_4-2x_5 &=0\\ 0=0 \end{align} \end{matrix}$$

• The general solution is $x_1 = 2x_2+x_4-3x_5, x_3 = -2x_4+2x_5$, with $x_2,x_4$, and $x_5$ free.

• Next, decompose the vector giving the general solution into a linear combination of vectors where the weights are the free variables. That is, $$\begin{align} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{bmatrix} &= \begin{bmatrix} 2x_2+x_4-3x_5 \\ x_2 \\ -2x_4+2x_5\\ x_4 \\ x_5 \end{bmatrix} \\ &= x_2 \begin{bmatrix} 2\\ 1\\ 0\\ 0\\ 0 \end{bmatrix} +x_4 \begin{bmatrix} 1\\ 0\\ -2\\ 1\\ 0 \end{bmatrix} +x_5 \begin{bmatrix} -3\\ 0\\ 2\\ 0\\ 1 \end{bmatrix} \\ &= x_2\textbf{u} +x_4 \textbf{v} + x_5 \textbf{w} \tag{3} \end{align}$$

• Every linear combination of $\textbf{u}$, $\textbf{v}$, and $\textbf{w}$ is an element of Nul $A$.

• Thus $\left\{ \textbf{u}, \textbf{v}, \textbf{w} \right\}$ is a spanning set for Nul $A$.
  1. The spanning set produced by the method in Example (3) is automatically linearly independent because the free variables are the weights on the spanning vectors.
  2. When Nul $A$ contains nonzero vectors, the number of vectors in the spanning set for Nul $A$ equals the number of free variables in the equation $A\textbf{x}=\textbf{0}$.

Definition : Column Space

The column space of an $m \times n$ matrix $A$, written as Col $A$, is the set of all linear combinations of the columns of $A$. If $A=\begin{bmatrix} \textbf{a}_1 & \cdots & \textbf{a}_n \end{bmatrix}$, then

$$\text{Col }A = \text{Span }\left\{ \textbf{a}_1, \cdots \textbf{a}_n\right\}.$$

Theorem 3:

The column space of an $m \times n$ matrix $A$ is a subspace of $\mathbb{R}^m$.

• A typical vector in Col $A$ can be written as $A\textbf{x}$ for some $x$ because the notation $A\textbf{x}$ stands for a linear combination of the columns of $A$. That is,

$$\text{Col }A = \left\{ \textbf{b}:\textbf{b}= A \textbf{x} \text{ for some }\textbf{x} \text{ in } \mathbb{R}^n \right\}$$

• The notation $A\textbf{x}$ for vectors in Col $A$ also shows that Col $A$ is the range of the linear transformation $\textbf{x} \mapsto A\textbf{x}$.
• The column space of an $m \times n$ matrix $A$ is all of $\mathbb{R}^m$ if and only if the equation $A\textbf{x}$ has a solution for each b in $\mathbb{R}^m$.

Example 7

Let $\displaystyle A=\left[\begin{matrix}2 & 4 & -2 & 1\\-2 & -5 & 7 & 3\\3 & 7 & -8 & 6\end{matrix}\right]$, $\displaystyle \textbf{u}= \left[\begin{matrix}3\\-2\\-1\\0\end{matrix}\right]$, and $\displaystyle \textbf{v}= \left[\begin{matrix}3\\-1\\3\end{matrix}\right]$.

• A)Determine if $\textbf{u}$ is in Nul $A$. Could $\textbf{u}$ be in Col $A$?
• B)Determine if $\textbf{v}$ is in Col $A$. Could $\textbf{v}$ be in Nul $A$?

Solution

A)

• An explicit description of Nul $A$ is not needed here. Simply compute the product $A\textbf{u}$.

$$A\textbf{u}=\left[\begin{matrix}2 & 4 & -2 & 1\\-2 & -5 & 7 & 3\\3 & 7 & -8 & 6\end{matrix}\right] \left[\begin{matrix}3\\-2\\-1\\0\end{matrix}\right] = \left[\begin{matrix}0\\-3\\3\end{matrix}\right] \ne \begin{bmatrix} 0 \\0 \\0 \end{bmatrix}$$

• $\textbf{u}$ is not a solution of $A\textbf{x}=\textbf{0}$, so $\textbf{u}$ is not in Nul $A$.
• Also, with four entries, $\textbf{u}$ could not possibly be in Col $A$, since Col $A$ is a subspace of $\mathbb{R}^3$.

B)

• Reduce $\begin{bmatrix} A & \textbf{v} \end{bmatrix}$ to an echelon form.

$$\begin{bmatrix} A & \textbf{v} \end{bmatrix} = \displaystyle \left[\begin{matrix}2 & 4 & -2 & 1 & 3\\-2 & -5 & 7 & 3 & -1\\3 & 7 & -8 & 6 & 3\end{matrix}\right] \sim \displaystyle \left[\begin{matrix}1 & 0 & 9 & 0 & 5\\0 & 1 & -5 & 0 & - \frac{30}{17}\\0 & 0 & 0 & 1 & \frac{1}{17}\end{matrix}\right]$$

• The equation $A\textbf{x}=\textbf{v}$ is consistent, so $\textbf{v}$ is in Col $A$.
• With only three entries, $v$ could not possibly be in Nul $A$, since Nul A is a subspace of $\mathbb{R}^n$

Contrast Between Nul $A$ and Col $A$ for an $m$ by $n$ Matrix $A$

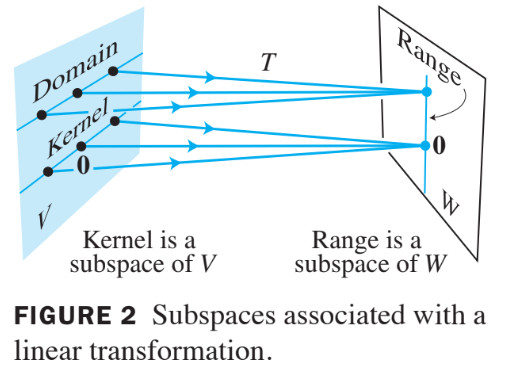
Kernel and Range of a Linear Transformation

Subspaces of vector spaces other than $\mathbb{R}^n$ are often described in terms of a linear transformation instead of a matrix.

Definition : Linear Transformation

A linear transformation $T$ from a vector space $V$ into a vector space $W$ is a rule that assigns to each vector $\textbf{x}$ in $V$ a unique vector in $W$, such that

1. $T(\textbf{u}+\textbf{v})=T(\textbf{u})+T(\textbf{v})$ for all $\textbf{u}$, $\textbf{v}$ in $V$, and
2. $T(c\textbf{u}) = cT(\textbf{u})$ for all $\textbf{u}$ in $V$ and all scalars $c$.

Definition : Kernel

The kernel (or null space) of such a $T$ is the set of all $\textbf{u}$ in $V$ such that $T(\textbf{u})=\textbf{0}$ (the zero vector in $W$).

• The kernel of $T$ is a subspace of $V$.

Definition : Range

The range of $T$ is the set of all vectors in $W$ of the form $T(\textbf{x})$ for some $\textbf{x}$ in $V$.

• The range of $T$ is a subspace of $W$.