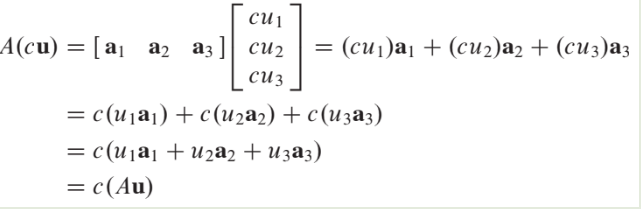Linear Equations in Linear Algebra

1.4 The Matrix Equation $A\textbf{x}$

A fundamental idea of linear algebra is to view a linear combination of vectors as the product of a matrix and a vector!!

Definition

If $A$ is an $m \times n$ matrix, with columns $\textbf{a}_1, \cdots, \bf{a}_n$, and if $\textbf{x}$ is in $\mathbb{R}^n$, then the product of $A$ and $\textbf{x}$, denoted by $A\bf{x}$ is the linear combination of the columns of $A$ using the corresponding entries in $\textbf{x}$ as weights; that is,

$$A\textbf{x} = \begin{bmatrix} & & \\ \textbf{a}_1 & \cdots & \textbf{a}_n\\ & & \\ \end{bmatrix} \begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix} = x_1 \textbf{a}_1 + x_2 \textbf{a}_2 + \cdots + x_n \textbf{a}_n$$

Note that $A\textbf{x}$ is defined only if the number of columns of $A$ equals the number of entries in $\textbf{x}$. .

Example 2

For $\textbf{v}_1, \bf{v}_2, \bf{v}_3$ in $\mathbb{R}^m$, write the linear combination $3\textbf{v}_1-5\textbf{v}_2+7\textbf{v}_3$ as a matrix times a vector.

Solution of Example 2

Place $\textbf{v}_1, \bf{v}_2, \bf{v}_3$ into the columns of a matrix $A$ and place the weights 3,-5, and 7 into a vector $\bf{x}$. That is,

$$3\textbf{v}_1-5\textbf{v}_2+7\textbf{v}_3=\begin{bmatrix} \textbf{v}_1 & \textbf{v}_2 & \textbf{v}_3 \end{bmatrix} \begin{bmatrix} 3 \\ -5 \\ 7 \end{bmatrix} = A \textbf{x}$$

$\blacksquare$

Now, write the system of linear equations as a vector equation involving a linear combination of vectors.

For examples, the following system

$$\begin{align} x_1+2x_2-x_3 &=4 \\ -5x_2 +3 x_3 &=1 \end{align} \tag{1}$$

is equivalent to

$$x_1 \begin{bmatrix} 1 \\ 0 \end{bmatrix} +x_2 \begin{bmatrix} 2 \\ -5 \end{bmatrix} +x_3 \begin{bmatrix} -1 \\ 3 \end{bmatrix} = \begin{bmatrix} 4 \\ 1 \end{bmatrix} \tag{2}$$

As in the example, the linear combination of the left side is a matrix times a vector, so that (2) becomes

$$\begin{bmatrix} 1 & 2 & -1 \\ 0 & -5 & 3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 4 \\ 1 \end{bmatrix} \tag{3}$$

Equation (3) has the form $A\textbf{x}=\bf{b}$. Such an equation is called a matrix equation to distinguish it from a vector equation such as shown in (2).

Theorem 3

If $A$ is an $m \times n$ matrix, with columns $\textbf{a}_1, \bf{a}_2, \cdots, \bf{a}_n$, and if $\bf{x}$ is in $\mathbb{R}^n$, then the matrix equation

$$A\textbf{x} = \bf{b}$$

has the same solution set as the vector equation.

$$x_1 \textbf{a}_1 + x_2 \textbf{a}_2 + \cdots + x_n \textbf{a}_n = \textbf{b}$$

which, in turn, has the same solution set as the systme of linear euqations whose augmented matrix is

$$\begin{bmatrix} \textbf{a}_1 & \bf{a}_2 & \cdots & \bf{a}_n & \bf{b} \end{bmatrix}$$

Existence of Solutions

• The equation $A\textbf{x} = \bf{b}$ has a solution if and only if $\bf{b}$ is a linear combination of the columns of $A$.

Theorem 4

Let $A$ be an $m \times n$ matrix. Then the following statements are logically equivalent. That is, for a particular $A$, either they are all true statements or they are all false.

1. For each $\textbf{b}$ in $\mathbb{R}^m$, the equation $A\bf{x}$ has a solution.
2. Each $\textbf{b}$ in $\mathbb{R}^m$ is a linear combination of the columns of $A$.
3. The columns of $A$ span $\mathbb{R}^m$
4. $A$ has a pivot position in every row.

• Theorem 4 is about a coefficient matrix, not an augmented matrix.

Example 4 : Computation of $A\textbf{x}$

Compute $A\textbf{x}$, where $\textbf{A} = \begin{bmatrix} 2 & 3 & 4 \\ -1 & 5 & -3 \\ 6 & -2 & 8 \end{bmatrix}$ and $\textbf{x} = \begin{bmatrix}x_1 \\ x_2 \\ x_3 \end{bmatrix}$.

Solution of Example 4

From the definition,

$$\begin{align} \begin{bmatrix} 2 & 3 & 4 \\ -1 & 5 & -3 \\ 6 & -2 & 8 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} &= x_1 \begin{bmatrix} 2 \\ -1 \\ 6 \end{bmatrix} +x_2 \begin{bmatrix} 3 \\ 5 \\ -2 \end{bmatrix} +x_3 \begin{bmatrix} 4 \\ -3 \\ 8 \end{bmatrix} \\ &= \begin{bmatrix} 2x_1 \\ -x_1 \\ 6x_1 \end{bmatrix} + \begin{bmatrix} 3x_2 \\ 5x_2 \\ -2x_2 \end{bmatrix} + \begin{bmatrix} 4x_3 \\ -3x_3 \\ 8x_3 \end{bmatrix} \\ &= \begin{bmatrix} 2x_1+3x_2+4x_3 \\ -x_1+5x_2-3x_3 \\ 6x_1-2x_2+8x_3 \end{bmatrix} \end{align} \tag{1}$$

The first entry in the product $A\textbf{x}$ is a sum of products (sometimes called a dot product), using the first row of $A$ and the entries in $\textbf{x}$.

That is,

$$\begin{bmatrix} 2 & 3 & 4 \\ & & \\ & & \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 2x_1+3x_2+4x_3 \\ \\ \\ \end{bmatrix}$$

Similarly, the second entry in $A\textbf{x}$ can be calculated by multiplying the entries in the second row of $A$ by the corresponding entries in $\textbf{x}$ and then summing the resulting products. $$\begin{bmatrix} & & \\ -1&5 &3 \\ & & \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} \\ -x_1+5x_2-3x_3 \\ \\ \end{bmatrix}$$

Likewise, the third entry in $A\textbf{x}$ can be calculated from the third row of $A$ and the entries in $\textbf{x}$ $\blacksquare$.

Row-Vector Rule for Computing $A\textbf{x}$

If the product $A\textbf{x}$ is defined, then the $i$-th entry in $A\bf{x}$ the sum of the products of corresponding entries from row $i$ of $A$ and from the vector $\textbf{x}$.

Identity Matrix

The matrix with 1’s on the diagonal and 0’s elsewhere is called an identity matrix and is denoted by $I$.

For example, $\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$ is an identity matrix.

Properties of the Matrix-Vector Product $A\textbf{x}$

The facts in the next theorem are important and will be used throughout the text. Think about Linearity.

Theorem 5

If $A$ is an $m \times n$ matrix, $\textbf{u}$ and $\bf{v}$ are vectors in $\mathbb{R}^n$, and $c$ is a scalar, then

1. $A(\textbf{u} +\bf{v}) = A\bf{u} +A\bf{v}$

2. $A(c\textbf{u}) = c(A\textbf{u})$

Proof of Theorem 5

For simplicity, take $n =3$, $A = \begin{bmatrix} a_1 & a_2 & a_3 \end{bmatrix}$, and $\textbf{u}$ and $\bf{v}$ in $\mathbb{R}^3$.

For $i=1,2,3$, let $u_i$ and $v_i$ be the $i$-th entries in $\textbf{u}$ and $\bf{v}$, respectively.

To prove statement (1), compute $A(\textbf{u}+\bf{v})$ as a linear combination of the columns of $A$ using the entries in $\textbf{u} + \bf{v}$ as weights.

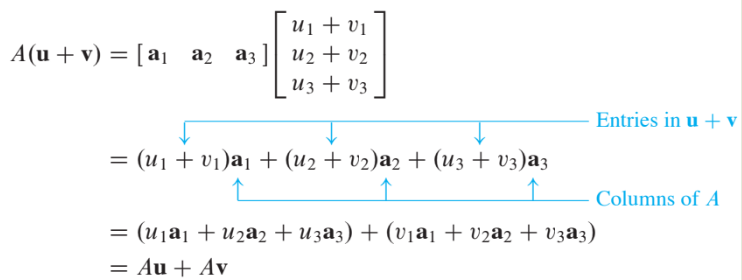
To prove statement (2), compute $A(c\textbf{u})$ as a linear combination of the columns of $A$ using the entries in $c\textbf{u}$ as weights.

$\blacksquare$