Ch02. Matrix Algebra

2.8 Subspaces of R to the Power n

Definition : Subspace of $R^n$

A subspace of $\mathbb{R}^n$ is any set $H$ in $\mathbb{R}^n$ that has three properties:

1. The zero vector is in $H$.
2. For each $\textbf{u}$ and $\textbf{v}$ in $H$, the sum $\textbf{u}+\textbf{v}$ is in $H$. : Addition
3. For each $\textbf{u}$ in $H$ and each scalar $c$, the vector $c\textbf{u}$ is in $H$. : Scalar Multiple

간단히는 vector space의 부분집합이라고 볼 수 있음.

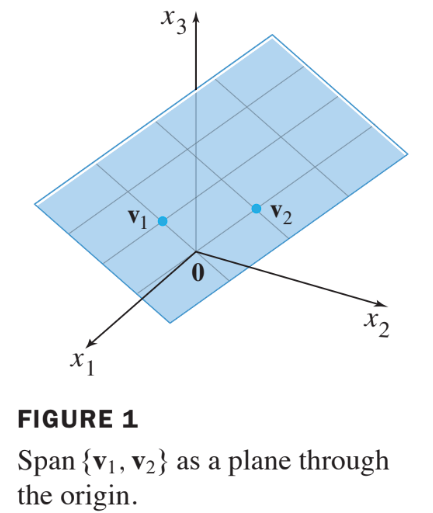
A plane through the origin is the standard way to visualization the subspace in $R^3$. See Fig. 1 below:

Example 1 :

If $\textbf{v}_1$ and $\textbf{v}_2$ are in $\mathbb{R}^n$ and $H=\text{Span}\left\{ \textbf{v}_1, \textbf{v}_2 \right\}$, then $H$ is a subspace of $\mathbb{R}^n$.

To verify this statement, note that the zero veocor is in $H$ (becuase $0\textbf{v}_1 + 0\textbf{v}_2$ is a linear combination of $\textbf{v}_1$ and $\textbf{v}_2$).

Solution.

• Now take two arbitrary vectors in $H$, say,

$$\textbf{u} = s_1 \textbf{v}_1 + s_2 \textbf{v}_2$$ and $$\textbf{v} = t_1 \textbf{v}_1 + t_2 \textbf{v}_2$$

Then $$\textbf{u+v} = (s_1+t_1) \textbf{v}_1 + (s_2+t_2) \textbf{v}_2$$

• which shows that $\textbf{u+v}$ is a linear combination of $\textbf{v}_1$ and $\textbf{v}_2$ and hence is in $H$.
• Also, for any scalar $c$, the vector $c\textbf{u}$ is in $H$, because $c\textbf{u}= c\left( s_1\textbf{v}_1 + s_2 \textbf{v}_2 \right) = cs_1\textbf{v}_1 + cs_2 \textbf{v}_2$.

Definition : Column Space

The column space of a matrix $A$ is the set $\text{Col }A$ of all linear combinations of the columns of $A$.

• If $A=\begin{bmatrix} \textbf{a}_1 \cdots \textbf{a}_n \end{bmatrix}$ with the columns of $\mathbb{R}^m$, then $\text{Col }A$ is the same as $\text{Span }\left\{\textbf{a}_1, \cdots, \textbf{a}_n \right\}$. Example 4 shows that the Column space of an $m \times n$ matrix is a subspace of $\mathbb{R}^m$.

Example 4:

Let $A=\begin{bmatrix} 1 & -3 & -4 \\ -4 & 6 & -2 \\ -3 & 7 & 6 \end{bmatrix}$ and $\textbf{b} = \begin{bmatrix} 3 \\ 3 \\ -4 \end{bmatrix}$.

Determine whether $\textbf{b}$ is in the column space of $A$

Solution:

• The vector $\textbf{b}$ is a linear combination of the columns of $A$ if and only if $\textbf{b}$ can be written as $A\textbf{x}$ for some $\textbf{x}$, that is, if and only if the equation $A\textbf{x}=\textbf{b}$ has a solution.
• Row reducing the augmented matrix $\begin{bmatrix} A & \textbf{b} \end{bmatrix}$, $$\begin{bmatrix} 1 & -3 &-4 & 3 \\ -4 & 6 & -2 & 3 \\ -3 & 7 & 6 & -4 \end{bmatrix} \sim \begin{bmatrix} 1 & -3 &-4 & 3 \\ 0 & -6 & -18 & 15 \\ 0 & -2 & -6 & 5 \end{bmatrix} \sim \begin{bmatrix} 1 & -3 &-4 & 3 \\ 0 & -6 & -18 & 15 \\ 0 & 0 & 0 & 0 \end{bmatrix}$$
• We conclude that $A\textbf{x}=\textbf{b}$ is consistent and $\textbf{b}$ is in $\text{Col }A$.

Definition : Null Space

The null space of a matrix $A$ is the set $\text{Nul }A$ of all solutions of the homogenous equation $A\textbf{x}=\textbf{0}$.

Theorem 12

The null space of an $m \times n$ matrix $A$ is a subspace of $\mathbb{R}^n$. Equivalently, the set of all solutions of a systme $A\textbf{x}=\textbf{0}$ of $m$ homogenous linear equations in $n$ unknowns is a subspace of $\mathbb{R}^n$.

Proof:

• The zero vector is in $\text{Nul }A$ (becuase $A\textbf{0}=\textbf{0}$).
• To show that $\text{Nul }A$ satisfies that other two properties required for a subspace, take any $\textbf{u}$ and $\textbf{v}$ in $\text{Nul }A$.
• That is, suppose $A\textbf{u}=\textbf{0}$ and $A\textbf{v}=\textbf{0}$. Then, by a property of matrix multiplication, $$A(\textbf{u}+\textbf{v}) = A\textbf{u} + A\textbf{v} = \textbf{0} + \textbf{0} = \textbf{0}$$
• Thus $\textbf{u}+\textbf{v}$ satisfies $A\textbf{x}=\textbf{0}$ and so $\textbf{u}+\textbf{v}$ is in $\text{Nul }A$. Also, for any scalar $c$,$A(c\textbf{u})=cA(\textbf{u})=c(\textbf{0})=\textbf{0}$, which shows that $c\textbf{u}$ is in $\text{Nul }A$.

Definition : Basis

A basis for a subspace $H$ of $\mathbb{R}^n$ is a linearly independent set in $H$ that spans $H$.

Example 5

The columns of an invertible $n \times n$ matrix form a basis for all of $\mathbb{R}^n$ because they are linearly independent and span $\mathbb{R}^n$ by the Invertible Matrix Theorem.

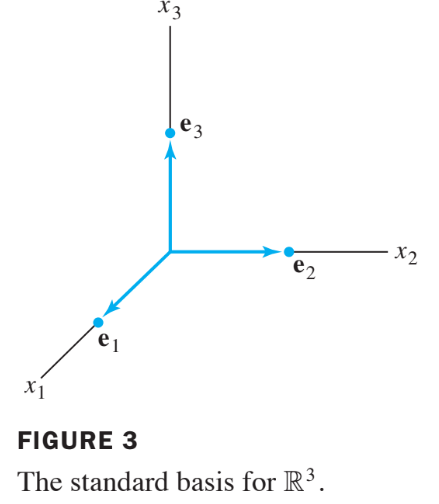
One such matrix is the $n \times n$ identity matrix. Its columns are denoted by $\textbf{e}_1, \cdots, \textbf{e}_n$:

$$\textbf{e}_1 = \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}, \textbf{e}_2 = \begin{bmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix}, \cdots \textbf{e}_n = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix}$$

• The set $\left\{\textbf{e}_1, \cdots, \textbf{e}_n\right\}$ is called the standard basis for $\mathbb{R}^n$. See Fig. 3 below.

Theorem 13:

The pivot columns of a matrix $A$ form a basis for the column space of $A$.