Ch04 Vector Space

4.1 Vector Spaces and Subspaces

Definition : Vector Space

A Vector space is a nonempty set $V$ of objects, called vectors,

on which are defined two operations, called

• addition and
• multiplication by scalars (real numbers),

subject to the ten axioms (or rules) listed below.

The axioms must hold for all vectors $\bf{u}$,$\bf{v}$, and $\bf{w}$ in $V$ for all scalars $c$ and $d$.

1. The sum of $\bf{u}$ and $\bf{v}$, denoted by $\textbf{u}+\textbf{v}$, is in $V$.
2. $\textbf{u}+\textbf{v} = \textbf{v}+\textbf{u}$ :commutative
3. $(\textbf{u}+\textbf{v})+\textbf{w} = \textbf{u} +(\textbf{v}+\textbf{w})$. :associative
4. There is a zero vector $\textbf{0}$ in $V$ such that $\textbf{u}+\textbf{0} = \textbf{u}$.
5. For each $\textbf{u}$ in $V$, there is a vector $-\textbf{u}$ in $V$ such that $\textbf{u}+(-\textbf{u})=\textbf{0}$.
6. The scalar multiple of $\textbf{u}$ by $c$, denoted by $c\textbf{u}$, is in $V$.
7. $c(\textbf{u}+\textbf{v}) = c\textbf{u} + c\textbf{v}$. :distributive
8. $(c+d)\textbf{u} = c\textbf{u} + d\textbf{u}$ :distributive
9. $c(d\textbf{u}) = (cd)\textbf{u}$. : associative
10. $1\textbf{u} = \textbf{u}$

Scalar를 real number로 제한하지 않고 complex number로 확장할 경우, complex vector space가 되며 $R$이 아닌 $C$ 상의 vector들을 다루게 된다.

Using these axioms, we can show that

• the zero vector in Axiom 4 is unique, and the vector $-\textbf{u}$, called the negative of $\textbf{u}$, in Axiom 5 is unique* for each $\textbf{u}$ in $V$.

For each $\textbf{u}$ in $V$ and scalar $c$,

$$0\textbf{u} = \textbf{0} \tag{1}$$ $c\textbf{0} = \textbf{0} \tag{2}$ $$-\textbf{u} = (-1)\textbf{u} \tag{3}$$

Example 2:

Let $V$ be the set of all arrows (directed line segments) in three-dimensional space, with two arrows regarded as equal if they have the same length and point in the same direction. Define addition by the parallelogram rule, and for each $\textbf{v}$ in $V$, define $c\textbf{v}$ to be the arrow whose length is $\lvert c \rvert$ times the length of $\textbf{v}$, pointing in the same direction as $\textbf{v}$ if $c \ge 0$ and otherwise pointing in the opposite direction.

See the following figure below. Show that $V$ is a vector space.

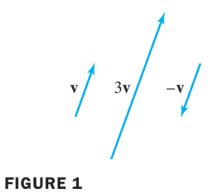
Solution:

• The definition of $V$ is geometric, using concepts of length and direction.
• No x y z-coordinate system is invovled.
• An arrow of zero length is a single point and represents the zero vector.
• The negative of $\textbf{v}$ is $(-1)\textbf{v}$.
• So Axioms 1, 4, 5, 6, and 10 are evident. See the figures below.

Definition

A subspace of a vector space $V$ is a subset $H$ of $V$ that has three properties:

1. The zero vector of $V$ is in $H$.
2. $H$ is closed under vector addtion. That is, for each $\bf{u}$ and $\bf{v}$ in $H$, the sum $\textbf{u}+\textbf{v}$ is in $H$.
3. $H$ is closed under multiplication by scalars. That is, for each $\bf{u}$ in $H$ and each scalar $c$, the vector $c\textbf{u}$ is in $H$.

• Properties (1), (2), and (3) guarantee that a subspace $H$ of $V$ is itself a vector space, under the vector space operations already defined in $V$.
• Every subspace is a vector space.
• Conversely, every vector space is a subspace (of itself and possibly of other larger spaces).

A Subspace Spanned by a Set

The set consisting of only the zero vector in a vector space $V$ is a subspace of $V$, called the zero subspace and written as $\left\{\textbf{0}\right\}$.

As the term liniear combination refers to any sum of scalar multiples of vectors, and $\text{Span }\left\{ \textbf{v}_1,\cdots,\textbf{v}_p\right\}$ denotes the set of all vectors that can be written as linear combinations of $\textbf{v}_1, \cdots, \textbf{v}_p$.

Example 10:

Given $\bf{v}_1$ and $\bf{v}_2$ in a vector space $V$, let $H=\text{Span }\left\{ \textbf{v}_1, \textbf{v}_2 \right\}$. Show that $H$ is a subspace of $V$.

Solution:

• The zero vector is in $H$, since $\textbf{0} = 0\textbf{v}_1 + 0\textbf{v}_2$.
• To show that $H$ is closed uncer vector addition, take two arbitrary vectors in $H$, say,

$$\textbf{u} = s_1 \textbf{v}_1 + s_2 \textbf{v}_2 \text{ and } \textbf{w} = t_1 \textbf{v}_1 + t_2 \textbf{v}_2.$$

• By Axioms 2,3, and 8 for the vector space $V$,

$$\begin{align} \textbf{u}+\textbf{w} &= (s_1 \textbf{v}_1 +s_2 \textbf{v}_2) + (t_1 \textbf{v}_1 + t_2 \textbf{v}_2) \\ &= (s_1 +t_1)\textbf{v}_1 + (s_2+t_2)\textbf{v}_2 \end{align}$$

• So $\textbf{u}+\textbf{v}$ is in $H$.

• Furthermore, if $c$ is any scalar, then by Axioms 7 and 9, $$\begin{align} c\textbf{u} &= c(s_1 \textbf{v}_1 + s_2 \textbf{v}_2) \\ &=(cs_1)\textbf{v}_1 + (cs_2)\textbf{v}_2 \end{align}$$ which shows that $c\textbf{u}$ is in $H$ and $H$ is closed under scalar multiplication.

• Thus $H$ is a subspace of $V$.

Theorem 1:

If $\textbf{v}_1, \cdots, \textbf{v}_p$ are in a vector space $V$, then $\text{Span }\left\{ \textbf{v}_1, \cdots, \textbf{v}_p \right\}$ is a subspace of $V$.

We call $\text{Span }\left\{ \textbf{v}_1, \cdots, \textbf{v}_p \right\}$ the subspace spanned (or **generated) by $\left\{ \textbf{v}_1, \cdots, \textbf{v}_p \right\}$.

Give any subspace $H$ and $V$, a spanning (or generating) set for $H$ is a set $\left\{ \textbf{v}_1, \cdots, \textbf{v}_p \right\}$ in $H$ such that

$$H = \text{Span }\left\{ \textbf{v}_1, \cdots \textbf{v}_p \right\}$$