Vector Spaces
4.4 Coordinae Systems
Theorem 7: The Unique Reresentation Theorem
Let be a basis for vector space . Then for each in , there exists a unique set of scalars such that
Proof:
- Since spans , there exist scalars such that (1) holds.
- Suppose also has the representation
for scalars .
- Then, subtracting, we have
- Since is linearly independent, the weights in (2) must all be zero. That is, for .
Definition:
- Suppose is a basis for and is in .
- The coordinates of relative to the basis (or the -coordinate of ) are the weights such that .
- If are the -coordinates of , then the vector in
is the coordinate vector of (relative to ), or the **-coordinate vector of .
The mapping is the coordinate mapping (determined by ).
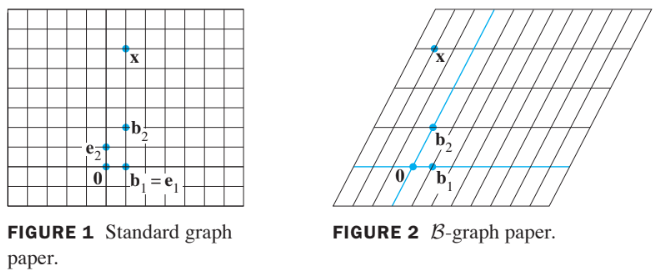
When a basis for is fixed, the -coordinate vector of a specified is easily found, as in the example below.
Example 1:
Let , and . Find the coordinate vector of relative to .
Solution:
- The -coordinate of satisfy
or
This equation can be solved by row operations on an augmented matrix or by using the inverse of the matrix on the left.
In any case, the solution is .
Thus and
- See the follwing figure.
The matrix in (3) changes the -coordinates of a vector into the standard coordinates for .
An analogous change of coordinates can be carried out in for a basis
Let
- Then the vector equation
is equivalent to
is called the change-of-coordinates matrix from to the standard basis in .
Left-multiplication by transforms the coordinate vector
into .Since the columns of form a basis for , is invertible (by the Invertible Matrix Theorem).
Left-multiplication by converts into its -coordinate vector:
The correspondence produced by , is the coordinate mapping.
Since , is an invertible matrix, the coordinate mapping is a one-to-one linear transformation from onto , by the Invertible Matrix Theorem.
Theorem 8 :
Let be a basis for a vector space . Then the coordinate mapping , is a one-to-one linear transformation from onto .
Proof :
- Take two typical vectors in , say,
- Then, using vector operations,
- It follows that
So the coordinate mapping preserves addition.
If is any scalar, then
- So
- Thus the coordinate mapping also preserves scalar multiplication and
hence is a linear transformation.
one-to-one and onto 증명은 숙제.
The linearity of the coordinate mapping can extend to linear combinations.
If are in and if are scalars, then
- In words, (5) says that the -coordinate vector of a linear combination of is the same linear combination of their coordinate vectors.
Isomorphism (동형사상)
The coordinate mapping in Theorem 8 is an important example of an isomorphism from onto .
- In general, a one-to-one linear transformation from a vector space onto a vector space is called an isomorphism from onto .
- The notation and terminology for and may differ, but the two spaces are indistinguishable as vector spaces.
- Every vector space calculation in is accurately reproduced in , and vice versa.
- In particular, any real vector space with a basis of vectors is indistinguishable from .
Example 5:
Example 7:
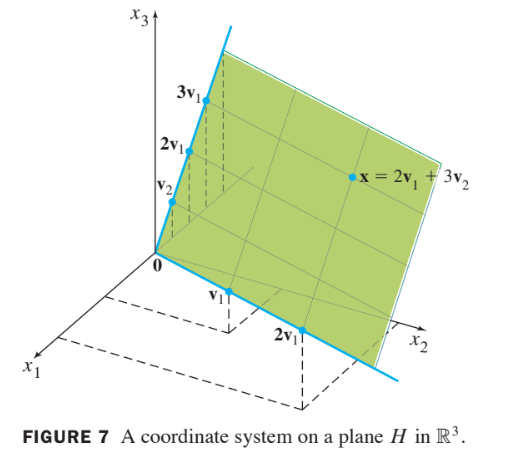
Let , and .
Then is a basis for .
Determine if is in , and if it is, find the coordinate vector of relative to .
Solution :
- If is in , then the following vector equation is consistent:
The scalars and , if they exist, are the - coordinates of .
Using row operations, we obtain
Thus and .
The coordinate system on determined by is shown in the following figure.