Ch02. Matrix Algebra

2.3 Characterizations of Invertible Matrices

The Invertible Matrix Theorem

Theorem 8 : The Invertible Matrix Theorem

Let $A$ be a square $n \times n$ matrix. Then the following statements are equivalent. That is, for a given $A$, the statements are either all true or all false.

• (1). $A$ is an invertible matrix.
• (2). $A$ is row equivalent to the identity matrix.
• (3). $A$ has $n$ pivot positions.
• (4). The equation $A \textbf{x}=\textbf{0}$ has only the trivial solution.
• (5). The columns of $A$ form a linearly independent set.
• (6). The linear transformation $\textbf{x} \mapsto A\textbf{x}$ is one-to-one.
• (7). The equation $A \textbf{x}=\textbf{b}$ has at least one solution for each $\textbf{b}$ in $\mathbb{R}^n$.
• (8). The columns of $A$ span $\mathbb{R}^n$.
• (9). The linear transformation $\textbf{x} \mapsto A\textbf{x}$ maps $\mathbb{R}^n$ onto $\mathbb{R}^n$.
• (10). There is an $n \times n$ matrix $C$ such that $CA=I$.
• (11). There is an $n \times n$ matrix $D$ such that $AD=I$.
• (12). $A^T$ is an invertible matrix.

• First, we need some notation.
• If the truth of statement (1) always implies that statement (10) is true, we say that (1) implies (10) and write $(1) \Rightarrow (10)$.
• The proof will establish the "circle" of implications as shown in the following figure.

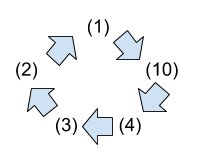
• If any one of these five statements is true, then so are the others.
• Finally, the proof will link the remaining statements of the theorem to the statements in this circle.

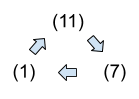
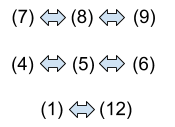
Proof:

• If statement (1) is true, then $A^{-1}$ works for $C$ in (10), so $(1) \Rightarrow (10)$.
• Next, $(10) \Rightarrow (4)$.
• Also, $(4) \Rightarrow (3)$.
• If $A$ is square and has $n$ pivot positions, then the pivots must lie on the main diagonal, in which case the reduced echelon form of $A$ is $I_n$. Thus $(3) \Rightarrow (2)$.
• Also, $(2) \Rightarrow (1)$.
• This completes the circle in the previous figure.

• Next, $(1) \Rightarrow (11)$ because $A^{-1}$ works for $D$.
• Also, $(11) \Rightarrow (7)$ and $(7) \Rightarrow (1)$.
• So, $(11)$ and $(7)$ are linked to the circle.

• Further, $(7), (8),$ and $(9)$ are equivalent for any matrix.
• Thus, $(8)$ and $(9)$ are linked through $(11)$ to the circle.
• Since $(4)$ is linked to the circle, so are $(5)$ and $(6)$, because $(4)$, $(5)$, and $(6)$ are all equivalent for any matrix $A$.
• Finally, $(1) \Rightarrow (12)$ and $(12) \Rightarrow (1)$.

This completes the proof. $\blacksquare$

Because of Theorem 5, Theorem 8 (7) could also be written as The equation $A\textbf{x} =\textbf{b}$ has a unique solution for each $\textbf{b}$ in $\mathbb{R}^n$.

• This statement implies (2) and hence implies that $A$ is invertible.

The following fact follows from Theorem 8. Let $A$ and $B$ be square matrices. If $AB=I$, then $A$ and $B$ are both invertible, with $B=A^{-1}$ and $A=B^{-1}$.

• The Invertible Matrix Theorem divides the set of all $n \times n$ matrices into two disjoint classes:
  • the invertible (nonsingular) matrices, and
  • the noninvertible (singular) matrices.
• Each statement in the theorem describes a property of every $n \times n$ invertible matrix.

• The negation(부정) of a statement in the theorem describes a property of every $n \times n$ singular matrix.
• For instance, an $n \times n$ singular matrix
  • is not row equivalent to $I_n$,
  • does not have $n$ pivot position, and
  • has linearly dependent columns.

Example 1:

Use the Invertible Matrix Theorem to decide if $A$ is invertible:

$$A= \begin{bmatrix} 1 & 0 & -2 \\ 3 & 1 & -2 \\ -5 & -1 & 9 \end{bmatrix}$$

Solution:

$$A \sim \begin{bmatrix} 1 & 0 & -2 \\ 0 & 1 & 4 \\ 0 & -1 & -1 \end{bmatrix} \sim \begin{bmatrix} 1 & 0 & -2 \\ 0 & 1 & 4 \\ 0 & 0 & 3 \end{bmatrix}$$

• So $A$ has three pivot positions and hence is invertible, by the Invertible Matrix Theorem, statement (3).
• The Invertible Matrix Theorem applies only to square matrices.
• For example, if the columns of a $4 \times 3$ matrix are linearly independent, we cannot use the Invertible Matrix Theorem to conclude anything about the existence or nonexistence of solutions of equation of the form $A\textbf{x}=\textbf{b}$.
• The next theorem shows that if such an $S$ exists, it is unique and must be a linear transformation. We call $S$ the inverse of $T$ and write it as $T^{-1}$

Invertible Linear Transformations

• Matrix multiplication corresponds to composition of linear transformations.

• When a matrix $A$ is invertible, the equation $A^{-1}A\textbf{x}=\textbf{x}$ can be viewed as a statement about linear transformations. See the following figure.

  

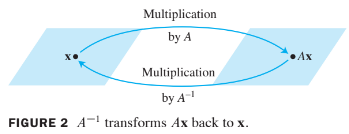
• A linear transformation $T: \mathbb{R}^n \rightarrow \mathbb{R}^n$ is said to be invertible if there exists a function $S: \mathbb{R}^n \rightarrow \mathbb{R}^n$ such that

  • $S(T(\textbf{x})) = \textbf{x}$ for all $\textbf{x}$ in $\mathbb{R}^n$. (1)
  • $T(S(\textbf{x})) = \textbf{x}$ for all $\textbf{x}$ in $\mathbb{R}^n$. (2)

Theorem 9:

Let $T: \mathbb{R}^n \rightarrow \mathbb{R}^n$ be a linear transformation and let $A$ be the standard matrix for $T$. Then $T$ is invertible if and only if $A$ is an invertible matrix. In that case, the linear transformation $S$ given by $S(\textbf{x})=A^{-1}\textbf{x}$ is the unique function satisfying equation (1) and (2).

Proof :

• Suppose that $T$ is invertible.
• Then (2) shows that $T$ is onto $\mathbb{R}^n$, for if $\bf{b}$ is in $\mathbb{R}^n$ and $\textbf{x}=S(\textbf{b})$, then $T(\textbf{x})=T(S(\textbf{b}))=\textbf{b}$, so each $\textbf{b}$ is in the range of $T$.
• Thus $A$ is invertible, by the Invertible Matrix Theorem, statement (9).
• Conversely, suppose that $A$ is invertible, and let $S(\textbf{x})=A^{-1}\textbf{x}$.
• Then, $S$ is a linear transformation, and $S$ satisfies (1) and (2).
• For instance, $S(T(\textbf{x})) = S(A\textbf{x})=A^{-1}(A\textbf{x})=\textbf{x}$.
• Thus, $T$ is invertible.