Ch02 Matrix Algebra

2.9 Dimension and Rank

Coodinate Systems

• Suppose $B=\left\{ \bf{b}_1, \cdots, \bf{b}_p \right\}$ is a basis for $H$, and suppose a vector $\textbf{x}$ in $H$ can be generated in two ways, say,

$$\textbf{x} = c_1 \textbf{b}_1 +\cdots + c_p \textbf{b}_p \text{ and } \textbf{x} = d_1 \textbf{b}_1 +\cdots + d_p \textbf{b}_p \tag{1}$$

• Then, subtracting gives

$$\textbf{0} = \textbf{x}-\textbf{x} = (c_1-d_1)\textbf{b}_1 + \cdots +(c_p-d_p)\textbf{b}_p \tag{2}$$

• Since $B$ is linearly independent, the weights in (2) must all be zero.
• That is, $c_j = d_j$ for $1 \le j \le p$, which shows that the two representations in (1) are actually the same.

Definition : Coordinate Vector

Suppose the set $B=\left\{ \bf{b}_1, \cdots, \bf{b}_p \right\}$ is a basis for a subspace $H$. For each $\textbf{x}$ in $H$, the coordinates of $\textbf{x}$ relative to the basis $B$ are the weights $c_1, \cdots, c_p$ such that $\textbf{x} = c_1 \textbf{b}_1 +\cdots + c_p \textbf{b}_p$, and the vector in $\mathbb{R}^p$

$$[\textbf{x}]_B = \begin{bmatrix} c_1 \\ \vdots \\ c_p \end{bmatrix}$$

is called the coordinate vector of x (relative to $B$) or the $B$-coordinate vector of x.

Example 1

Let $\textbf{v}_1=\begin{bmatrix}3 \\ 6\\ 2 \end{bmatrix}$, $\textbf{v}_2=\begin{bmatrix}-1 \\ 0\\ 1 \end{bmatrix}$, $\textbf{x}=\begin{bmatrix}3 \\ 12\\ 7 \end{bmatrix}$, and $B=\left\{ \bf{v}_1, \bf{v}_2 \right\}$. Then $B$ is a basis for $H= \text{Span }\left\{ \bf{v}_1, \bf{v}_2 \right\}$ because $\textbf{v}_1$ and $\textbf{v}_2$ are linearly independent. Determine if $\bf{x}$ is in $H$, and if it is , find the coordinate vector of $\bf{x}$ relative to $B$.

Solution

• If $\bf{x}$ is in $H$, then the following vector equation is consistent:

$$c_1 \begin{bmatrix} 3\\ 6\\ 2 \end{bmatrix} + c_2 \begin{bmatrix} -1 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 3 \\ 12 \\ 7 \end{bmatrix}$$

• The scalars $c_1$ and $c_2$, if they exist, are the $B$-coordinates of $\textbf{x}$. Row operations show that

$$\begin{bmatrix} 3 & -1 & 3 \\ 6 & 0 & 12 \\ 2 & 1 & 7 \end{bmatrix} \sim \begin{bmatrix} 1 & 0 & 2 \\ 0 & 1 & 3 \\ 0 & 0 & 0 \end{bmatrix}$$

• Thus $c_1=2, c_2=3$ and $[\textbf{x}]_B= \begin{bmatrix}2 \\3 \end{bmatrix}$.
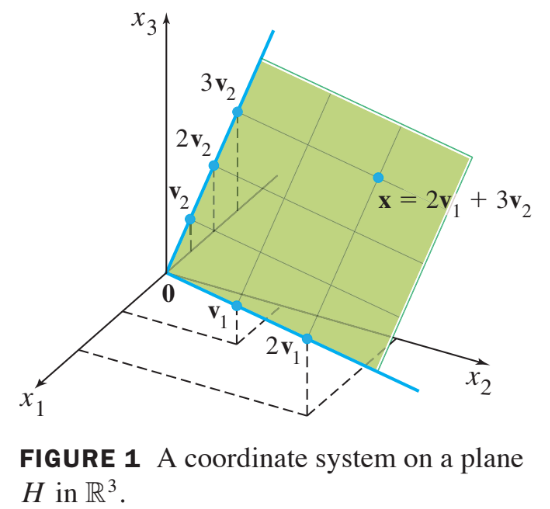
• The basis $B$ determines a “coordinate system” on $H$, which can be visualized by the grid shown in Fig. 1 below.

Definition: Dimension

The dimension of a nonzero subspace $H$, denoted by dim $H$, is the number of vectors in any basis for $H$. The dimension of the zero subspace ${\textbf{0} }$ is defined to be zero.

Definition: Rank

The rank of a matrix $A$, denoted by rank $A$, is the dimension of the column space of $A$.

Example 3 :

Determine the rank of the matrix

$$A \sim \begin{bmatrix} 2 & 5 & -3 & -4 & 8 \\ 0 & -3 & 2 & 5 & -7 \\ 0 & -6 & 4 & 14 & -20 \\ 0 & -9 & 6 & 5 & -6 \end{bmatrix}$$

Solution :

Reduce $A$ to echelon form :

• The matrix $A$ has 3 pivot columns, so rank $A$ = 3.

Theorem 14 : Rank Theorem

If a matrix $A$ has $n$ columns, then rank $A$ + dim $\text{Nul }A = n$.

Theorem 15 :

Let $H$ be a $p$-dimensional subspace of $\mathbb{R}^n$. Any linearly independent set of exactly $p$ elements in $H$ is automatically a basis for $H$. Also, any set of $p$ elements of $H$ that spans $H$ is automatically a basis for $H$.

Theorem : The Invertible Theorem (continued) :

Let $A$ be an $n \times n$ square matrix. Then the following statements are each equivalent to the statement that $A$ is an invertible matrix.

• (13) The columns of $A$ form a basis of $\mathbb{R}^n$
• (14) $\text{Col }A = \mathbb{R}^n$
• (15) dim $\text{Col }A = n$
• (16) rank $A = n$
• (17) $\text{Nul }A = \left\{\textbf{0}\right\}$
• (18) dim $\text{Nul }A = 0$

Proof

• Statement (13) is logically equivalent to statements (5) and (8) regarding linear independence and spanning.
• The other five statements are linked to the earlier ones of the theorem by the following chain of almost trivial implications: $$(7) \Rightarrow (14) \Rightarrow (15) \Rightarrow (16) \Rightarrow (18) \Rightarrow (17) \Rightarrow (4)$$
• Statement (7), which says that the equation $A\textbf{x}=\textbf{b}$ has at least one solution for each $\bf{b}$ in $\mathbb{R}^n$, implies statement (14), because $\text{Col }A$ is precisely the set of all $\textbf{b}$ such that the equation $A\textbf{x}=\textbf{b}$ is consistent.
• The implications $(14) \Rightarrow (15) \Rightarrow (16)$ follow from the definitions of dimension and rank.
• If the rank of $A$ is $n$, the number of columns of $A$, then dim $\text{Nul }A = 0$, by the Rank Theorem, and so $\text{Nul }A= \left\{\textbf{0}\right\}$. Thus $(16) \Rightarrow (18) \Rightarrow (17)$.
• Also, statement (17) implies that the equation $A\textbf{x}=\textbf{0}$ has only the trivial solution, which is statement (4).
• Since statements (4) and (7) are already known to be equivalent to the statement that $A$ is invertible, the proof is complete.