Orthogonality and Least Square
6.1 Inner Product, Length, and Orthogonality
Inner Prodcut
- If and are vectors in , then we regard and as matrices.
- The transpose is a matrix, and the matrix product is an matrix, which we write as a single real number (a scalar) without brackets.
- The number is called the inner product of and , and it is written as .
- This inner product is also referred to as a dot product
- If and ,
- then the inner product of and is
Theorem 1
Let , and be vectors in , and let be a scalar. Then
- , and if and only if
Properties (2) and (3) can be combined several times to produce the following useful rule:
The Length of a Vector
If is in , with entries , then the square root of is defined because is non-nengative.
Definition of Length
The length (or norm) of is the nonnegative scalar defined by
, and
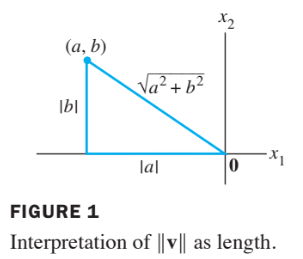
- Suppose is in , say
- If we identify with a geometric point in the plane, as usual, then coincides with the standard notion of the length of the line segment from the origin to .
- This follows from the Pythagorean Theorem applied to a triangle such as the one shown in the following figure 1.
- For any scalar , the length is times the length of . That is
- A vector whose length is 1 is called a unit vector.
- If we divide a nonzero vector by its length -that is, multiply by - we obtain a unit vector because the length of is .
- The process of creating , from is sometimes called normalizing , and we say that , is in the same direction as .
Example 2:
Let . Find a unit vector in the same direction as .
Solution:
- First, compute the length of :
- Then, multiply by to obtain
Distance in
Definintion of Distance
For and in , the distance between and , written as , is the length of the vector . That is
Example 4:
Compute the distance between the vectors and .
Solution of Example 4
- Calculate
- The vectors ,, and are shown in the figure below.
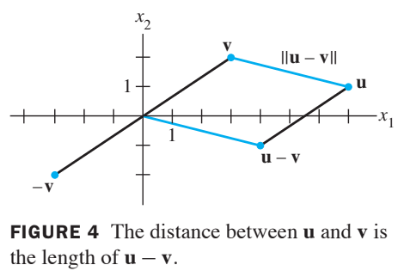
- When the vector is added to , the result is .
Notice that the parallelogram in the above figure shows that the distance from to is the same as the distance from to .
Orthogonal Vectors
- Consider or and two lines through the origin dertermined by vectors and .
- See the figure below.
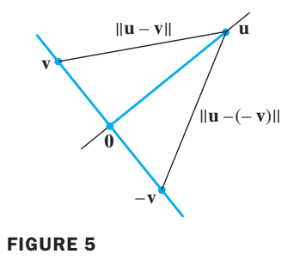
- The two lines shown in the figure above are geomatrically perpendicular if and only if the distance from to is the same as the distance from to .
- This is the same as requiring the squares of the distances to be the same.
- Now
- The same calculations with and interchanged show that
- The two squared distances are equal if and only if , which happens if and only if .
This calculation shows that when vectors and are identified with geometric points, the corresponding lines through the points and the origin are perpendicular if and only if .
Definition of Orthogonality
Two vectors and in are orthogonal (to each other) if .
- The zero vector is orthgonal to every vector in becuase for all .
Theorem 2
Two vectors and are orthogonal if and only if .
Orthogonal Complements
If a vector is orthogonal to every vector in a subspace of , then is said to be orthogonal to .
The set of all vectors that are orthogonal to is called the orthogonal complement of and is denoted by (and read as “W perpendicular” or simply “W perp”).
- A vector is in if and only if is orthogonal to every vector in a set that spans .
- is a subspace of
Theorem 3
Let be an matrix. The orthogonal complement of the row space of is the null space of , and the orthogonal complement of the column space of is the null space of :
Proof:
- The row-column rule for computing shows that if is in , then is orthogonal to each row of (with the rows treated as vectors in ).
- Since the rows of span the row space, is orthogonal to .
- Conversely, if is orthogonal to , then is certainly orthogonal to each row of , and hence
- This proves the first statement of the theorem.
- Since this statement is true for any matrix, it is true for .
- That is, the orthogonal complement of the row space of is the null space of
- This proves the second statement, because Row = Col .
Angles In R Squared and R Cubed (Optional)
- If and are nonzero vectors in either or , then there is a nice connection between their inner product and the angle between the two line segments from the origin to the points identified with and .
- The formula is
- To verify this formula for vectors in , consider the triangle shown in the figure below with sides of lengths, ,, and .
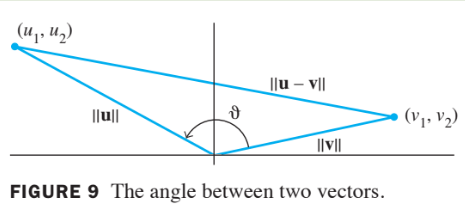
- By the law of cosines,
- which can be rearranged to produce the equations below
- The verification for is similar.
- When , formula (2) may be used to define the angle between two vectors in .
- In statistics, the value of defined by (2) for suitable vectors and is called a correlation coefficient.