Chapter 1. Linear Equations in Linear Algebra

1.9 The Matrix of a Linear Transformation

The Matrix of a Linear Transformation

Theorem 10:

Let $T: \mathbb{R}^n \rightarrow \mathbb{R}^m$ be a linear transformation. Then there exists a unique matrix $A$ such that $$T(\textbf{x})= A\textbf{x} \text{ for all} \textbf{x} \in \mathbb{R}^n$$

In fact, $A$ is the $m \times n$ matrix whose $j$th column is the vector $T(\textbf{e}_j)$, where $\textbf{e}_j$ is the $j$th column of the identity matrix in $\mathbb{R}^n$ $$A=\begin{bmatrix}T(\textbf{e}_1)& \cdots &T(\textbf{e}_n)\end{bmatrix} \tag{3}$$

Proof:

Write $\textbf{x}= I_n\textbf{x} =\begin{bmatrix}\textbf{e}_1& \cdots &\textbf{e}_n\end{bmatrix}\textbf{x} =x_1\textbf{e}_1 +\cdots+x_2\textbf{e}_n$, and

use the linearity of $T$ to compute

$$\begin{align} T(\textbf{x}) &= T(x_1\textbf{e}_1 +\cdots+x_2\textbf{e}_n)\\ &= x_1T(\textbf{e}_1) + \cdots + x_nT(\textbf{e}_n)\\ &= \begin{bmatrix}T(\textbf{e}_1)& \cdots &T(\textbf{e}_n)\end{bmatrix} \begin{bmatrix}x_1 \\ \vdots \\x_n\end{bmatrix} \\ &= A\textbf{x} \end{align}$$

유일성에 대한 증명은 생략(연습문제) $\blacksquare$

• The matrix A in (3) is called the standard matrix for the linear transformation $T$.
• We know now that every linear transformation from $\mathbb{R}^n$ to $\mathbb{R}^m$ can be viewed as a matrix transformation, and vice versa.
  • The term linear transformation focuses on a property of a mapping,
  • while matrix transformation describes how such a mapping is implemented.

Example 2:

Find the standard matrix $A$ for the dilation transformation $T(\textbf{x})=3\textbf{x}$, for $\textbf{x} \in \mathbb{R}^2$.

Solution:

Write

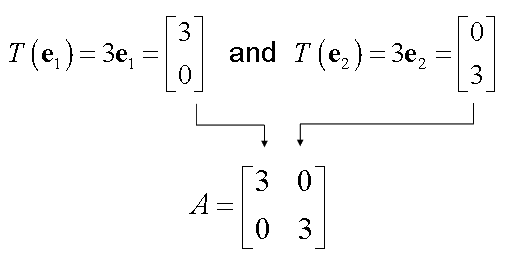
Existence and Uniqueness Questions

Tables 1-4 illustrate other common geometric linear transformations of the plane.

Table 1. Reflections

Transformation	Image of the Unit Square	Standard Matrix
Reflecting through the 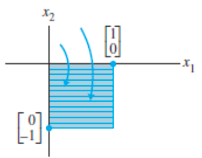$x_1$-axis		$\begin{bmatrix}1&0\\0&-1\end{bmatrix}$
Reflecting through the $x_2$-axis		$\begin{bmatrix}-1&0\\0&1\end{bmatrix}$
Reflecting through the line $x_2=x_1$		$\begin{bmatrix}0&1\\1&0\end{bmatrix}$
Reflecting through the line $x_2=-x_1$		$\begin{bmatrix}0&-1\\-1&0\end{bmatrix}$
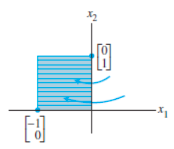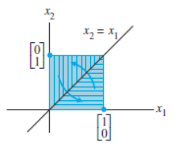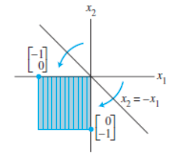Reflecting through the origin		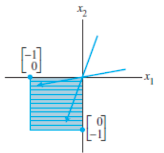$\begin{bmatrix}-1&0\\0&-1\end{bmatrix}$

Table 2. Contractions and Expansions

Transformation	Image of the Unit Square	Standard Matrix
Horizontal contraction and expansion		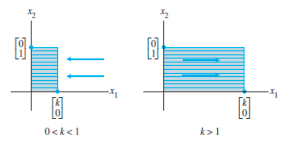$\begin{bmatrix}k&0\\0&1\end{bmatrix}$
Vertical contraction and expansion		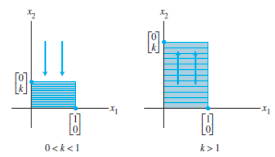$\begin{bmatrix}1&0\\0&k\end{bmatrix}$

Table 3. Shears

Transformation	Image of the Unit Square	Standard Matrix
Horizontal shear		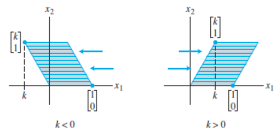$\begin{bmatrix}1&k\\0&1\end{bmatrix}$
Vertical shear		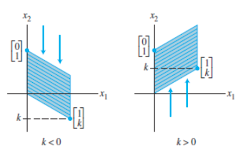$\begin{bmatrix}1&0\\k&1\end{bmatrix}$

Table 4. Projections

Transformation	Image of the Unit Square	Standard Matrix
Projection onto the $x_1$-axis		$\begin{bmatrix}1&0\\0&0\end{bmatrix}$
Projection onto the $x_2$-axis		$\begin{bmatrix}0&0\\0&1\end{bmatrix}$

Definition : onto (전사)

A mapping $T: \mathbb{R}^n \rightarrow \mathbb{R}^m$ is said to be onto(전사) $\mathbb{R}^m$ if each $\textbf{b}$ in $\mathbb{R}^m$ is the image of at least one $\textbf{x}$ in $\mathbb{R}^n$.

• Equivalently, $T$ is onto $\mathbb{R}^m$ when the range of $T$ is all of the codomain $\mathbb{R}^m$.
• That is, $T$ maps $\mathbb{R}^n$ onto $\mathbb{R}^m$ if, for each $\textbf{b}$ in the codomain $\mathbb{R}^m$, there exists at least one solution of $T(\textbf{x})=\textbf{b}$.
• Dose $T$ map $\mathbb{R}^n$ onto $\mathbb{R}^m$ is an existence question.
• The mapping $T$ is not onto when there is some $\textbf{b}$ in $\mathbb{R}^m$ for which the equation $T(\textbf{x})=\textbf{b}$ has no solution.
• See the figure below.

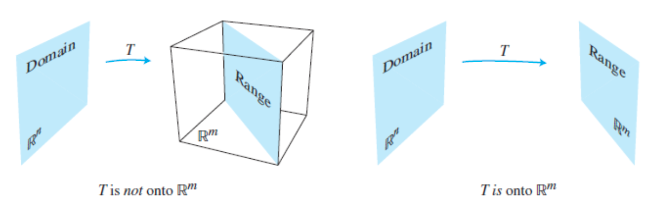
Figure 3. Is the range of $T$ all of $\mathbb{R}^m$?

Definition : one-to-one

Definition: A mapping $T: \mathbb{R}^n \rightarrow \mathbb{R}^m$ is said to be one-to-one(일대일) if each $\textbf{b}$ in $\mathbb{R}^m$ is the image of at most one $\textbf{x}$ in $\mathbb{R}^n$.

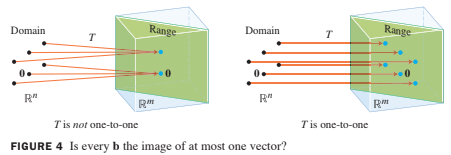
Example 4:

Let $T$ be the linear transformation whose standard matrix is $$A= \begin{bmatrix} 1 & -4 & 8 & 1 \\ 0 & 2 & -1 & 3 \\ 0 & 0 & 0 & 5 \\ \end{bmatrix}$$

Does $T$ map $\mathbb{R}^4$ onto $\mathbb{R}^3$

Is $T$ a one-to-one mapping?

Solution of Example 4:

Since $A$ happens to be in echelon form, we can see at once that $A$ has a pivot position in each row. By Theorem 4 in Section 1.4, for each $\textbf{b}$ in the equation $A\textbf{x}=\textbf{b}$ is consistent. In other words, the linear transformation $T$ maps $\mathbb{R}^4$(its domain) onto $\mathbb{R}^3$.

However, since the equation $A\textbf{x}=\textbf{b}$ has a free variable (because there are four variables and only three basic variables), each $\textbf{b}$ is the image of more than one $\textbf{x}$. This is, $T$ is not one-to-one. $\blacksquare$

Theorem 11:

Let $T: \mathbb{R}^n \rightarrow \mathbb{R}^m$ be a linear transformation.

Then $T$ is one-to-one if and only if the equation $A\textbf{x}=\textbf{0}$ has only the trivial solution.

Proof of Theorem 11:

Since T is linear, $T(\textbf{0})=\textbf{0}$. If $T$ is one-to-one, then the equation $T(\textbf{x})=\textbf{0}$ has at most one solution and hence only the trivial solution.

If $T$ is not one-to-one, then there is a $\textbf{0}$ that is the image of at least two different vectors in $\mathbb{R}^n$ --say, $\textbf{u}$ and $\textbf{v}$. That is $T(\textbf{u})=\textbf{b}$ and $T(\textbf{v})=\textbf{b}$. But then, since $T$ is linear, $$T(\textbf{u}-\textbf{v})=T(\textbf{u})-T(\textbf{v})=\textbf{b}-\textbf{b}=\textbf{0}$$

The vector $\textbf{u} − \textbf{u}$ is not zero, since $\textbf{u} \ne \textbf{u}$. Hence the equation $T(\textbf{x})=\textbf{0}$ has more than one solution. So, either the two conditions in the theorem are both true or they are both false.

Theorem 12:

Let $T: \mathbb{R}^n \rightarrow \mathbb{R}^m$ be a linear transformation and let $A$ be the standard matrix for $T$. Then:

1. $T$ maps $\mathbb{R}^n$ onto $\mathbb{R}^m$ if and only if the columns of $A$ span $\mathbb{R}^m$;
2. $T$ is one-to-one if and only if the columns of $A$ are linearly independent.

Proof of Theorem 12

1.

By Theorem 4 in Section 1.4, the columns of $A$ span $\mathbb{R}^m$ if and only if for each $\textbf{b}$ in $\mathbb{R}^m$ the equation $A\textbf{x}=\textbf{b}$ is consistent—in other words, if and only if for every $\textbf{b}$,the equation $T(\textbf{x})=\textbf{b}$ has at least one solution. This is true if and only if $T$ maps $\mathbb{R}^n$ onto $\mathbb{R}^m$.

2.

The equations $T(\textbf{x})=\textbf{0}$ and $A\textbf{x}=\textbf{0}$ are the same except for notation. So, by Theorem 11, $T$ is one-to-one if and only if $A\textbf{x}=\textbf{0}$ has only the trivial solution. This happens if and only if the columns of $A$ are linearly independent.