Vector Spaces

4.7 Chage of Basis

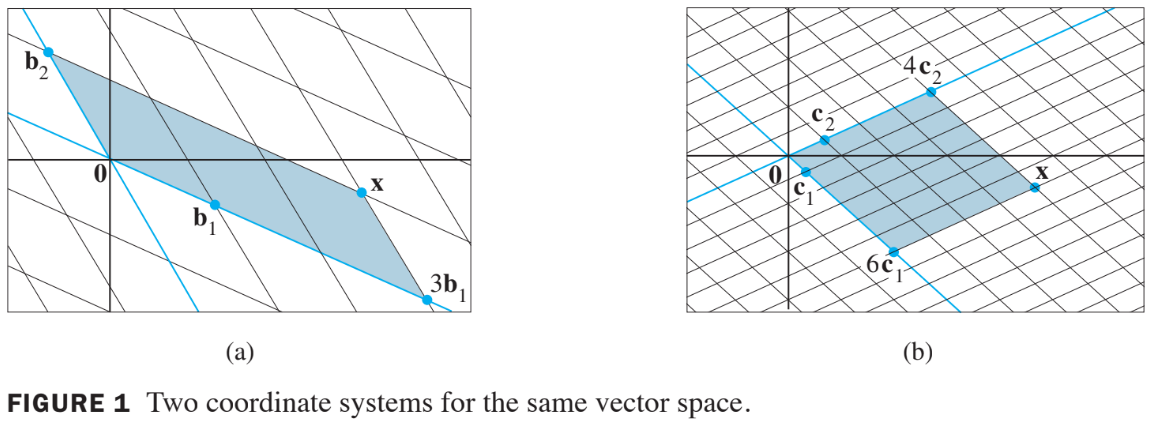
Example 1

Consider two bases $B=\left\{ \textbf{b}_1, \textbf{b}_2 \right\}$ and $C=\left\{ \textbf{c}_1, \textbf{c}_2 \right\}$ for a vector space $V$, such that $$\textbf{b}_1 = 4\textbf{c}_1 +\textbf{c}_2 \text{ and } \textbf{b}_2 = -6\textbf{c}_1 +\textbf{c}_2 \tag{1}$$

Suppose $$\textbf{x} = 3 \textbf{b}_1 +\textbf{b}_2 \tag{2}$$

That is, suppose $[\textbf{x}]_B = \begin{bmatrix}3 \\ 1 \end{bmatrix}$.

Find $[\textbf{x}]_C$.

Solution

• Apply the coordinate mapping determined by $C$ to $\textbf{x}$ in (2). Since the coordinate mapping is a linear transformation,

$$\begin{align} [\textbf{x}]_C &= [3\textbf{b}_1 +\textbf{b}_2]_C \\ &= 3[\textbf{b}_1]_C +[\textbf{b}_2]_C \end{align}$$

• We can write the vector equation as a matrix equation, using the vectors in the linear combination as the columns of a matrix:

$$[\textbf{x}]_C = \begin{bmatrix} [\textbf{b}_1]_C & [\textbf{b}_2]_C \\ \end{bmatrix} \begin{bmatrix} 3 \\ 1 \end{bmatrix} \tag{3}$$

• This formula gives $[\textbf{x}]_C$, once we know the columns of the matrix. From (1),

$$[\textbf{b}_1]_C = \begin{bmatrix} 4 \\ 1 \end{bmatrix} \text{ and } [\textbf{b}_2]_C = \begin{bmatrix} -6 \\ 1 \end{bmatrix}$$

• Thus, (3) provides the solution:

$$[\textbf{x}]_C = \begin{bmatrix} 4 & -6 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 3 \\ 1 \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \end{bmatrix}$$

• The $C$-coordinates of $\textbf{x}$ match those of the $\textbf{x}$ in Fig.1, as seen on the below.

Theorem 15:

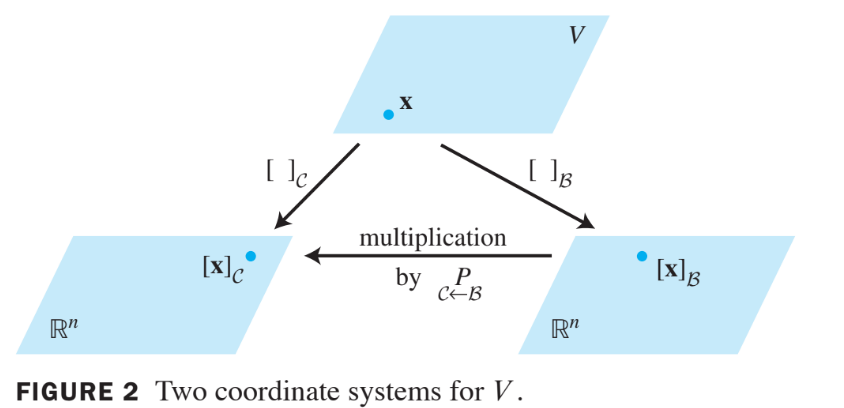
Let $B=\left\{ \textbf{b}_1, \cdots, \textbf{b}_n \right\}$ and $C=\left\{ \textbf{c}_1, \cdots, \textbf{c}_n \right\}$ be bases of a vector space $V$. Then there is a unique $n \times n$ matrix $\underset{C \leftarrow B}{P}$ such that

$$[\textbf{x}]_C = \underset{C \leftarrow B}{P}[\textbf{x}]_B \tag{4}$$

The columns of $\underset{C \leftarrow B}{P}$ are the $C$-coordinate vectors of the vectors in the basis $B$. That is,

$$P_{C\leftarrow B} = \begin{bmatrix} [\textbf{b}_1]_C & [\textbf{b}_2]_C & \cdots &[\textbf{b}_n]_C \end{bmatrix} \tag{5}$$

• The matrix $\underset{C \leftarrow B}{P}$ in Theorem 15 is called the change-of-coordinates matrix from $B$ to $C$.
• Multiplication by $\underset{C \leftarrow B}{P}$ converts $B$-coordinates into $C$-coordinates.
• Figure 2 below illustrates the change-of-coordinates equation (4).

• The columns of $\underset{C \leftarrow B}{P}$ are linearly independent because they are the coordinate vectors of the linearly independent set $B$.
• Since $\underset{C \leftarrow B}{P}$ is square, it must be invertible, by the Invertible Matrix Theorem.
• Left-multiplying both sides of equation (4) by $\left(\underset{C \leftarrow B}{P}\right)^{-1}$ yields

$$\left(\underset{C \leftarrow B}{P}\right)^{-1} [\textbf{x}]_C = [\textbf{x}]_B$$

• Thus $\left(\underset{C \leftarrow B}{P}\right)^{-1}$ is the matrix that converts $C$-coordinates into $B$-coordinates. That is,

$$\left( \underset{C \leftarrow B}{P}\right)^{-1} = \underset{B \leftarrow C}{P} \tag{6}$$

Change of Basis in $\mathbb{R}^n$

• If $B=\left\{ \textbf{b}_1, \cdots, \textbf{b}_n \right\}$ and $\epsilon$ is the standard basis $\left\{ \textbf{e}_1, \cdots, \textbf{e}_n \right\}$ in $\mathbb{R}^n$, then $[\textbf{b}_1]_\epsilon = \textbf{b}_1$, and likewise for the other vectors in $B$. In this case, $\underset{\epsilon \leftarrow B}{P}$ is the same as the change-of-coordinates matrix $P_B$ introduced in Section 4.4, namely,

$$P_B = \begin{bmatrix} \textbf{b}_1 & \textbf{b}_2 & \cdots & \textbf{b}_n \end{bmatrix}.$$

• To change coordinates between two nonstandard bases in $\mathbb{R}^n$, we need Theorem 15. The theorem shows that to solve the change-of-basis problem, we need the coordinate vectors of the old basis relative to the new basis.

Example 2

Let $\textbf{b}_1 = \begin{bmatrix}-9 \\ 1 \end{bmatrix}, \textbf{b}_2 = \begin{bmatrix}-5 \\ -1 \end{bmatrix}, \textbf{c}_1 = \begin{bmatrix} 1 \\ -4 \end{bmatrix}, \textbf{c}_2 = \begin{bmatrix} 3 \\ -5 \end{bmatrix}$ and consider the bases for $\mathbb{R}^2$ given by $B=\left\{ \textbf{b}_1, \textbf{b}_2 \right\}$ and $C=\left\{ \textbf{c}_1, \textbf{c}_2 \right\}$.

Find the change-of-coordinates matrix from $B$ to $C$.

Solution

• The matrix $P_{B \leftarrow C}$ involves the $C$-coordinate vectors of $\textbf{b}_1$ and $\textbf{b}_2$. Let $[\textbf{b}_1]_C = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$ and $[\textbf{b}_2]_C = \begin{bmatrix} y_1 \\ y_2 \end{bmatrix}$.
• Then by defintion,

$$\left[\begin{matrix} c_1 & c_2 \\ \end{matrix} \right] \left[\begin{matrix} x_1 \\ x_2 \\ \end{matrix} \right] = \textbf{b}_1 \text{ and }$$ $$\left[\begin{matrix} c_1 & c_2 \\ \end{matrix} \right] \left[\begin{matrix} y_1 \\ y_2 \\ \end{matrix} \right] = \textbf{b}_2$$

• To solve both systems simultaneously, augment the coefficient matrix with $\textbf{b}_1$ and $\textbf{b}_2$, and row reduce:

$$\left[ \begin{array}{cc:cc} c_1 & c_2 & b_1 & b_2 \\ \end{array} \right] = \left[ \begin{array}{cc:cc} 1 & 3 & -9 & -5 \\ -4 & -5 & 1 & -1 \end{array} \right] \sim \left[ \begin{array}{cc:cc} 1 & 0 & 6 & 4 \\ 0 & 1 & -5 & -3 \end{array} \right] \tag{7}$$

• Thus

$$[\textbf{b}_1]_C = \begin{bmatrix} 6 \\-5 \end{bmatrix} \text{ and } [\textbf{b}_2]_C = \begin{bmatrix} 4 \\-3 \end{bmatrix}$$

• The desired change-of-coordinates matrix is therefore

$$P_{C \leftarrow B} = \begin{bmatrix} [\textbf{b}_1]_C & [\textbf{b}_2]_C \end{bmatrix} = \begin{bmatrix} 6 & 4 \\ -5 & -3 \end{bmatrix}$$