Chapter 1. Linear Equations in Linear Algebra

1.3 Vector Equations

Important properites of linear algebra can be described with the concept and notation of vectors.

The term vector appears in a variety of fields, which will be discussed in Chapter 4, Vector Space.

Until then, vector will mean an ordered list of numbers .

Vectors in $\mathbb{R^2}$

• A matrix with only one column is called a column vector, or simply a vector.
• An example of a vector with two entries is $$\textbf{w}=\begin{bmatrix}w_1 \\ w_2\end{bmatrix},$$
  • where $w_1$ and $w_2$ are any real numbers.
• The set of all vectors with two entries is denoted by $\mathbb{R^2}$ (read "r-two").
• The $\mathbb{R}$ stands for the real numbers that appear as entries in the vector, and the exponent 2 indicates that vecotr contains two entries.
• Two vectors in $\mathbb{R^2}$ are equal if and only if their corresponding entires are equal.
• Given two vectors $\textbf{u}$ and $\textbf{v}$ in $\mathbb{R^2}$, their sum is the vector $\textbf{u}+\textbf{v}$ obtained by adding corresponding entries $\textbf{u}$ and $\textbf{v}$.
• Given a vector $\textbf{u}$ and a real number $c$, the scalar multiple of $\textbf{u}$ by $c$ is the vector $c\textbf{u}$ obtained by multiplying each entry in $\textbf{u}$ by $c$

Example 1:

Gieven $\textbf{u}=\begin{bmatrix} 1 \\ -2 \end{bmatrix}$ and $\textbf{v}=\begin{bmatrix} 2 \\ -5 \end{bmatrix}$, find $4\textbf{u}$,$(-3)\textbf{v}$, and $4\textbf{u}+(-3)\textbf{v}$.

Solution of Example 1

$4\textbf{u}=\begin{bmatrix} 4 \\ -8 \end{bmatrix}$, $-3\textbf{v}=\begin{bmatrix} -6 \\ 15 \end{bmatrix}$, and

$4\textbf{u}+(-3)\textbf{v}= \begin{bmatrix} 4 \\ -8 \end{bmatrix} + \begin{bmatrix} -6 \\ 15 \end{bmatrix} = \begin{bmatrix} -2 \\ 7 \end{bmatrix}$

Geometric Descriptions of R Squared

• Consider a rectangular coordinate system in the plane. Because each point in the plane is determined by an ordered pair of numbers, we can identify a geometric point (a, b) with the column vector $\begin{bmatrix} a \\ b \end{bmatrix}$.
• So we may regard $\mathbb{R^2}$ as the set of all points in the plane.

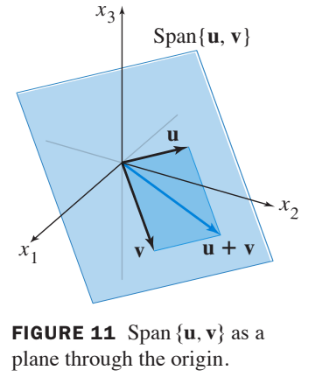
Parallelogram Rule for Addition

• If $\textbf{u}$ and $\textbf{v}$ in $\mathbb{R^2}$ are represented as points in the palne, then $\textbf{u}+\textbf{v}$ corresponds to the forth vertex of the parallelogram whose other vertices are $\textbf{u}$,$0$, and $\textbf{v}$. See Fig. 3 below.

Vectors in R cubed and R to the Power n

• Vectors in $\mathbb{R^3}$ are $3 \times 1$ coulumn metrices with three entries.
• They are represented geometrically by points in a three-dimensional coordinate space, with arrows from the origin sometimes included for visual clarity.
• If $n$ is a positive integer, $\mathbb{R}^n$ (read "r-n") denotes the collection of all lists (or ordered $n$-tuples) of $n$ real numbers, usually written as $n \times 1$ column matrices, such as $$\textbf{u}=\begin{bmatrix}u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix}$$

Algebraic Properties of R to the Power n

• The vector whose entries are all zero is called the zero vector and is denoted by $\textbf{0}$.
• For all $\textbf{u},\textbf{v},\textbf{w}$ in $\mathbb{R^n}$ and all scalar $c$ and $d$:
  1. $\textbf{u}+\textbf{v}=\textbf{v}+\textbf{u}$
  2. $(\textbf{u}+\textbf{v})+\textbf{w}=\textbf{u}+(\textbf{v}+\textbf{w})$
  3. $\textbf{u}+\textbf{0}=\textbf{0}+\textbf{u}=\textbf{u}$
  4. $\textbf{u}+(-\textbf{u})=-\textbf{u}+\textbf{u}=\textbf{0}$, where $-\textbf{u}$ denotes $(-1)\textbf{u}$
  5. $c(\textbf{u}+\textbf{v})= c\textbf{u}+c\textbf{v}$
  6. $(c+d)\textbf{u} = c\textbf{u}+d\textbf{u}$
  7. $c(d\textbf{u})=(cd)(\textbf{u})$
  8. $1 \textbf{u}= \textbf{u}$

Linear Combinations

Given vectors $\textbf{v}_1,\textbf{v}_2,\cdots,\textbf{v}_p$ in $\mathbb{R^n}$ and given scalars $c_1,c_2,\cdots,c_p$, the vector $\textbf{y}$ defined by

$$\textbf{y}=c_1\textbf{v}_1+\cdots+c_p \textbf{v}_p$$

is called a linear combination of $\textbf{v}_1,\textbf{v}_2,\cdots,\textbf{v}_p$ with weights $c_1,c_2,\cdots,c_p$.

• The weights in a linear combination can be any real numbers, including zero.

Exampel 5:

Let $\textbf{a}_1=\begin{bmatrix}1 \\ -2 \\ -5 \end{bmatrix}$, $\textbf{a}_2=\begin{bmatrix}2 \\ 5 \\ 6 \end{bmatrix}$ and $\textbf{b}=\begin{bmatrix}7 \\ 4 \\ -3 \end{bmatrix}$

Determine whether $\textbf{b}$ can be generated (or written) as a linear combination of $\textbf{a}_1$ and $\textbf{a}_2$. That is, determine whether weights $x_1$ and $x_2$ exist such that

$$x_1\textbf{a}_1+x_2\textbf{a}_2 = \textbf{b} \tag{1}$$

If vector equation (1) has a solution, find it.

Solution of Example 5

Use the definitions of scalar multiplication and vector addition to rewrite the vector equation

$$x_1\begin{bmatrix}1 \\ -2 \\ -5 \end{bmatrix} + x_2\begin{bmatrix}2 \\ 5 \\ 6 \end{bmatrix} = \begin{bmatrix}7 \\ 4 \\ -3 \end{bmatrix}$$

which is same as

$$\begin{bmatrix} x_1 \\ -2x_1 \\ -5x_1 \end{bmatrix} + \begin{bmatrix} 2x_2 \\ 5 x_2 \\ 6 x_2 \end{bmatrix} = \begin{bmatrix} 7 \\ 4 \\ -3 \end{bmatrix}$$

and

$$\begin{bmatrix} x_1 +2x_2\\ -2x_1 +5x_2 \\ -5x_1+6x_2 \end{bmatrix} = \begin{bmatrix} 7 \\ 4 \\ -3 \end{bmatrix} \tag{2}$$

• The vectors on the left and right sides of (2) are equal if and only if their corresponding entries are both equal. That is, $x_1$ and $x_2$ make the vector equation (1) true if and only if $x_1$ and $x_2$ satisfy the following system

$$\begin {align} x_1 +2x_2 &= 7 \\ -2x_1 +5 x_2 &= 4 \\ -5 x_1 + 6 x_2 &= -3 \end {align} \tag{3}$$

• To solve this system, row reduce the augmented matrix of the system as follows:

$$\begin {bmatrix} 1 & 2 & 7 \\ -2 & 5 & 4 \\ -5 & 6 & -3 \end {bmatrix} \sim \begin {bmatrix} 1 & 2 & 7 \\ 0 & 9 & 18 \\ 0 & 16 & 32 \end {bmatrix} \sim \begin {bmatrix} 1 & 2 & 7 \\ 0 & 1 & 2 \\ 0 & 16 & 32 \end {bmatrix} \sim \begin {bmatrix} 1 & 0 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \end {bmatrix}$$

• The solution of (3) is $x_1=3$ and $x_2=2$. Hence $\textbf{b}$ is a linear combination of $\textbf{a}_1$ and $\textbf{a}_2$, with weights $x_1=3$ and $x_2=2$. That is,

$$3 \begin{bmatrix} 1 \\ -2 \\ -5 \end{bmatrix} + 2 \begin{bmatrix} 2 \\ 5 \\ 6 \end{bmatrix} = \begin{bmatrix} 7 \\ 4 \\ -3 \end{bmatrix}$$

$\blacksquare$

In the Example 5, the original vectors $\bf{a}_1, \bf{a}_2$, and $\bf{b}$ are the columns of the augmented matrix that we row reduced:

• Write this matrix in a way that identifies its columns.

$$\begin{bmatrix} \textbf{a}_1 & \textbf{a}_2 & \textbf{b} \end{bmatrix} \tag{4}$$

• A vector equation $x_1\textbf{a}_1+x_2\textbf{a}_2+\cdots+x_n\textbf{a}_n = \textbf{b}$ has the same solution set as the linear system whose augmented matrix is

$$\begin{bmatrix} \textbf{a}_1 & \textbf{a}_2 & \cdots & \textbf{a}_n & \textbf{b} \end{bmatrix} \tag{5}$$

• In particular, $\textbf{b}$ can be generated by a linear combination of $\textbf{a}_1,\cdots,\textbf{a}_n$ if and only if there exists a solution to the linear system corresponding to the matrix (5).

Definition:

If $\textbf{v}_1, \cdots, \textbf{v}_p$ are in $\mathbb{R^n}$, then the set of all linear combinations of $\textbf{v}_1, \cdots, \textbf{v}_p$ is denoted by Span $\left\{\textbf{v}_1, \cdots, \textbf{v}_p\right\}$ and is called the subset of $\mathbb{R^n}$ Spanned (or generated) by $\textbf{v}_1, \cdots, \textbf{v}_p$. That is, Span $\left\{\textbf{v}_1, \cdots, \textbf{v}_p\right\}$ is the collection of all vectors that can be written in the form

$$c_1 \textbf{v}_1 +c_2 \textbf{v}_2 +\cdots + c_p \textbf{v}_p$$

with $c_1, \cdots, c_p$ scalars.

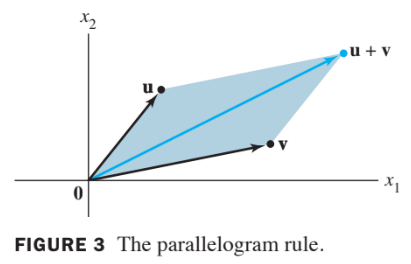
A Geometric Description of Span{v}

Let $\textbf{v}$ be a nonzero vector in $\mathbb{R^3}$. Then Span $\left\{\textbf{v}\right\}$ is the set of all scalar multiples of $\textbf{v}$, which is the set of points on the line in $\mathbb{R^3}$ through $\textbf{v}$ and $\textbf{0}$.

See Fig. 10 below:

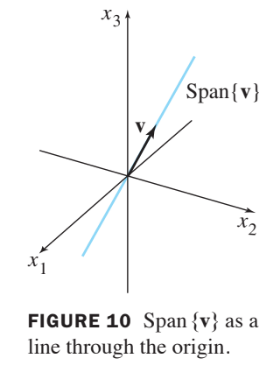
A Geometric Description of Span {u,v}

If $\textbf{u}$ and $\textbf{v}$ are nonzero vector in $\mathbb{R^3}$, with $\textbf{v}$ not a multiple of $\textbf{u}$, then Span $\left\{ \textbf{u},\textbf{v} \right\}$ is the plane in $\mathbb{R^3}$ that contains $\textbf{u}$, $\textbf{v}$, and $\textbf{0}$. In particular, Span $\left\{ \textbf{u}, \textbf{v} \right\}$ contains the line in $\mathbb{R^3}$ through $\textbf{u}$ and $\textbf{0}$ and the line through $\textbf{v}$ and $\textbf{0}$.

See Fig. 11 below: