2.7 Applications to Computer Graphics

• Computer graphics are images displayed or animated on a computer screen.
• Applications of computer graphics are widespread and growing rapidly.
• For instance, computer aided design (CAD) is an integral part of many engineering processes.

Most interactive computer software for business and industry makes use of computer graphics in the screen displays and for other functions, such as

• graphical display of data,
• desktop publishing, and
• slide production for commercial and educational presentations.

Consequently, anyone studying a computer language invariably spends time learning how to use at least two-dimensional (2D) graphics.

This section examines some of the basic mathematics used to manipulate and display graphical images.

• Often, curved lines are approximated by short straight-line segments, and
• a figure is defined mathematically by a list of points.

EXAMPLE 1

The capital letter N in Figure 1 is determined by eight points, or vertices. The coordinates of the points can be stored in a data matrix, $D$.

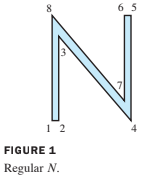
In addition to $D$, it is necessary to specify which vertices are connected by lines, but we omit this detail.

The main reason graphical objects are described by collections of straight-line segments is that the standard transformations in computer graphics map line segments onto other line segments.

Once the vertices that describe an object have been transformed, their images can be connected with the appropriate straight lines to produce the complete image of the original object.

EXAMPLE 2

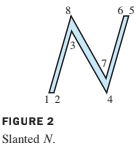
Given $A=\begin{bmatrix} 1 & .25 \\ 0 & 1 \end{bmatrix}$, describe the effect of the shear transformation $\textbf{x} \mapsto A\textbf{x}$ on the letter $N$ in Example 1.

Solution

By definition of matrix multiplication, the columns of the product AD contain the images of the vertices of the letter N.

$\displaystyle AD = \left[\begin{matrix}0 & 0.5 & 2.105 & 6 & 8.0 & 7.5 & 5.895 & 2.0\\0 & 0 & 6.42 & 0 & 8 & 8 & 1.58 & 8\end{matrix}\right]$

The transformed vertices are plotted in Figure 2, along with connecting line segments that correspond to those in the original figure.

The mathematics of computer graphics is intimately connected with matrix multiplication. Unfortunately, translating an object on a screen does not correspond directly to matrix multiplication because translation is not a linear transformation. The standard way to avoid this difficulty is to introduce what are called homogeneous coordinates.

Homogeneous Coordinates

Each point $(x,y)$ in $\mathbb{R}^2$ can be identified with the point $(x,y,1)$ on the plane in $\mathbb{R}^3$ that lies one unit above the $xy$-plane.

We say that $(x,y)$ has homogeneous coordinates $(x, y, 1)$.

• For instance, the point (0, 0) has homogeneous coordinates (0, 0, 1).

Homogeneous coordinates for points are not added or multiplied by scalars, but they can be transformed via multiplication by $3 \times 3$ matrices.

Translation

In homogeneous coordinates, the translation can be computed via matrix multiplication:

$\left[\begin{matrix}1 & 0 & h\\0 & 1 & k\\0 & 0 & 1\end{matrix}\right] \begin{bmatrix}x \\y \\ 1\end{bmatrix} = \begin{bmatrix}x+h \\y+k \\ 1\end{bmatrix}$

Example 5

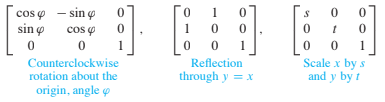
Any linear transformation on $\mathbb{R}^2$ is represented with respect to homogeneous coordinates by a partitioned matrix of the form $\begin{bmatrix}A & 0 \\ 0 & 1\end{bmatrix}$, where $A$ is a $2\times 2$ matrix. Typical examples are

Composite Transformations

• The movement of a figure on a computer screen often requires two or more basic transformations.
• The composition of such transformations corresponds to matrix multiplication when homogeneous coordinates are used.

EXAMPLE 6

Find the $3 \times 3$ matrix that corresponds to the composite transformation of a scaling by .3, a rotation of $90^\circ$ about the origin, and finally a translation that adds (-.5, 2) to each point of a figure.

Solution

If $\phi = \pi/2$, then $\sin{\phi}=1$ and $\cos{\phi}=0$. From Examples 4 and 5, we have

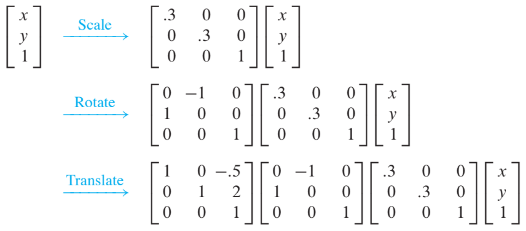
The matrix for the composite transformation is

$\begin{aligned} \begin{bmatrix} 1 & 0 & -.5 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0 & -1 & 0\\ 1 & 0 & \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} .3 & 0 & 0 \\ 0 & .3 & 0 \\ 0 & 0 & 1 \end{bmatrix} &= \begin{bmatrix} 0 & -1 & -.5 \\ 1 & 0 & 2 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} .3 & 0 & 0 \\ 0 & .3 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ &= \begin{bmatrix} 0 & -.3 & -.5\\ .3 & 0 & 2\\ 0 & 0 & 1\\ \end{bmatrix} \end{aligned}$

Homogeneous 3D Coordinates

By analogy with the 2D case, we say that $(x, y, z, 1)$ are homogeneous coordinates for the point $(x, y, z)$ in $\mathbb{R}^3$. In general, $(X, Y, Z, H)$ are homogeneous coordinates for $(x, y, z)$ if $H \ne 0$ and

$\begin {aligned} x &= \frac{X}{H}\\ y &= \frac{Y}{H}\\ z &= \frac{Z}{H} \end {aligned}$

• Each nonzero scalar multiple of $(x, y, z, 1)$ gives a set of homogeneous coordinates for $(x, y, z)$
• For instance, both (10,-6,14, 2) and (-15, 9,-21,-3) are homogeneous coordinates for (5,-3,7).

EXAMPLE 7 :

Give $4\times 4$ matrices for the following transformations:

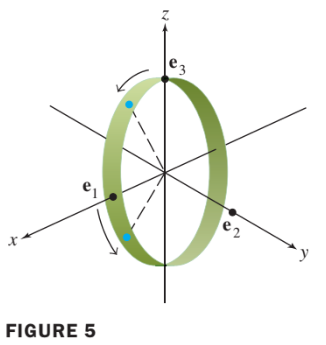
• a. Rotation about the y-axis through an angle of $30^\circ$. (By convention, a positive angle is the counterclockwise direction when looking toward the origin from the positive half of the axis of rotation—in this case, the y-axis.)
• b. Translation by the vector $\textbf{p}=(-6,4,5)$.

Solution

a.

First, construct the $3 \times 3$ matrix for the rotation.

• The vector $\textbf{e}_1$ rotates down toward the negative $z$-axis, stopping at $(\cos{30^\circ},0,-\sin{30^\circ}) = (\sqrt{3}/2,0,-.5)$.
• The vector $\textbf{e}_2$ on the $y$-axis does not move, but
• $\textbf{e}_3$ on the $z$-axis rotates down toward the positive $x$-axis, stopping at $(\sin{30^\circ},0,\cos{30^\circ}) = (.5,0,\sqrt{3}/2)$.
• See Figure 5. From Section 1.9, the standdard matrix for this rotation is

$\begin{bmatrix} \sqrt{3}/2 & 0 & .5 \\ 0 & 1 & 0 \\ -.5 & 0 & \sqrt{3}/2 \end{bmatrix}$

So the rotation matrix for homogeneous coordinates is

$A=\begin{bmatrix} \sqrt{3}/2 & 0 & .5 &0\\ 0 & 1 & 0 &0\\ -.5 & 0 & \sqrt{3}/2 &0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

b.

We want $(x, y, z, 1)$ to map to $(x-6, y+4, z+5, 1)$. The matrix that does this is

$\begin{bmatrix} 1 & 0 & 0 &-6 \\ 0 & 1 & 0 & 4 \\ 0 & 0 & 1 & 5 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

Perspective Projections

A three-dimensional object is represented on the two-dimensional computer screen by projecting the object onto a viewing plane. (We ignore other important steps, such as selecting the portion of the viewing plane to display on the screen.)

For simplicity, let

• the $xy$-plane represent the computer screen, and imagine that
• the eye of a viewer is along the positive $z$-axis, at a point $(0,0,d)$.

A perspective projection maps each point $(x, y, z)$ onto an image point $(x^*,y^*,0)$ so that the two points and the eye position, called the center of projection, are on a line. See Figure 6(a).

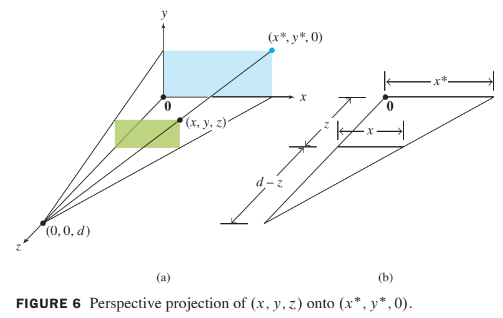
The triangle in the $xz$-plane in Figure 6(a) is redrawn in part (b) showing the lengths of line segments. Similar triangles show that

$\begin{aligned} \frac{x^*}{d}&=\frac{x}{d-z} \\ x^* &= \frac{dx}{d-z}=\frac{x}{1-z/d} \end{aligned}$

Similarly,

$y^*=\frac{y}{1-z/d}$

Using homogeneous coordinates, we can represent the perspective projection by a matrix, say, $P$. We want $(x,y,z,1)$ to map into $\left( \frac{x}{1-z/d},\frac{y}{1-z/d},0,1\right)$. Scaling these coordinates by $1-z/d$, we can also use $(x,y,0,1-z/d)$ as homogeneous coordinates for the images. Now it is easy to display $P$. In fact,

$P \begin{bmatrix} x \\y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 &0 &0 \\0&1&0&0 \\ 0&0&0&0 \\ 0&0&-1/d&1 \end{bmatrix} \begin{bmatrix} x \\y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x \\y \\ 0 \\ 1-z/d \end{bmatrix}$