Chapter 1. Linear Equations in Linear Algebra

1.8 Introduction to Linear Transformations

Linear Transformations

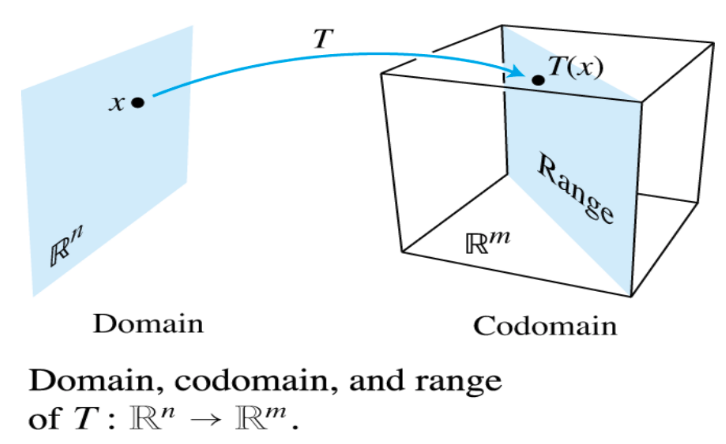
A transformation (or function or mapping) $T$ from $\mathbb{R}^n$ to $\mathbb{R}^m$ is a rule that assigns each vector $\textbf{x}$ in $\mathbb{R}^n$ to a vector $T(\textbf{x})$ in $\mathbb{R}^m$.

• The set $\mathbb{R}^n$ is called domain of $T$, and $\mathbb{R}^m$ is called codomain of $T$.
• The notation $T: \mathbb{R}^n \rightarrow \mathbb{R}^m$ indicates that the domain of $T$ is $\mathbb{R}^n$ and the codomain is $\mathbb{R}^m$.
• For $\textbf{x} \in \mathbb{R}^n$, the vector $T(\textbf{x}) \in \mathbb{R}^m$ is called the image of $\textbf{x}$(under the action of $T$).
• The set of all images $T(\textbf{x})$ is called the range of $T$. See Fig. 2 below.

Matrix Transformations

• For each $\textbf{x} \in \mathbb{R}^n$, $T(\textbf{x})$ is computed as $A\textbf{x}$, where $A$ is an $m\times n$ matrix.
• For simplicity, we denote such a matrix transformation by $\textbf{x} \mapsto A\textbf{x}$.
• Observe that the domain of $T$ is $\mathbb{R}^n$ when $A$ has $n$ columns and the codomain of $T$ is $\mathbb{R}^m$ when each column of $A$ has $m$ entries.
• The range of $T$ is the set of all linear combinations of the columns of $A$, because each image $T(\textbf{x})$ is of the form $A\textbf{x}$.

Example 1:

Let $A=\begin{bmatrix} 1 & -3 \\ 3 & 5 \\ -1 & 7 \end{bmatrix}, \textbf{u} =\begin{bmatrix} 2 \\ -1\end{bmatrix}, \textbf{b} =\begin{bmatrix} 3 \\ 2 \\ -5 \end{bmatrix}, \textbf{c} =\begin{bmatrix} 3 \\ 2 \\ 5\end{bmatrix}$ and define a transformation $T: \mathbb{R}^2 \mapsto \mathbb{R}^3$ by $T(\textbf{x})=A\textbf{x}$, so that $T(\textbf{x})=A\textbf{x}=\begin{bmatrix} 1 & -3 \\ 3 & 5 \\ -1 & 7 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} =\begin{bmatrix} x_1-3x_2 \\ 3x_1 + 5x_2 \\ -1x_1 + 7x_2 \end{bmatrix}$.

1. Find $T(\textbf{u})$, the image of $\textbf{u}$ under the transformation $T$
2. Find $\textbf{x} \in \mathbb{R}^2$ whose image under $T$ is $\textbf{b}$.
3. Is there more than one $\textbf{x}$ whose image under $T$ is $\textbf{b}$?
4. Determine if $\textbf{c}$ is in the range of the transformation $T$.

Solution of Example 1

1. Compute

$$T(\textbf{u})=A\textbf{u}=\begin{bmatrix} 1 & -3 \\ 3 & 5 \\ -1 & 7 \end{bmatrix}\begin{bmatrix} 2 \\ -1\end{bmatrix}=\begin{bmatrix} 5 \\ 1 \\ -9 \end{bmatrix}$$

2. Solve $T(\textbf{x})=\textbf{b}$ for $\textbf{x}$. That is, solve $A\textbf{x}=\textbf{b}$, or $$\begin{bmatrix} 1 & -3 \\ 3 & 5 \\ -1 & 7 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 3 \\ 2 \\ -5 \end{bmatrix} \tag{1}$$

• Row reduce the augmented matrix:$\begin{bmatrix} 1 & -3 & 3 \\ 3 & 5 & 2\\ -1 & 7 &-5\end{bmatrix} \sim \begin{bmatrix} 1 & -3 &3 \\ 0 & 14 & -7\\ 0 & 4 & -2\end{bmatrix} \sim \begin{bmatrix} 1 & -3 &3 \\ 0 & 1 & -.5\\ 0 & 0 & 0\end{bmatrix} \sim \begin{bmatrix} 1 & 0 & 1.5 \\ 0 & 1 & -.5\\ 0 & 0 & 0\end{bmatrix} \tag{2}$
• Hence $x_1=1.5, x_2=-.5, \text{ and } \textbf{x}=\begin{bmatrix} 1.5\\ -.5\end{bmatrix}$.
• The image of this $\textbf{x}$ under $T$ is the given vector $\textbf{b}$

3. Any $\textbf{x}$ whose image under $T$ is $\textbf{b}$ must satisfy equation (1).

• From (2), it is clear that equation (1) has a unique solution.
• So there is exactly one $\textbf{x}$ whose image is $\textbf{b}$.

4. The vector $\textbf{c}$ is in the range of $T$ if $\textbf{c}$ is the image of some $\textbf{x}$ in $\mathbb{R}^2$, that is, if $\textbf{c}=T(\textbf{x})$ for some $\textbf{x}$.

• This is another way of asking if the system $A\textbf{x}=\textbf{c}$ is consistent.
• To find the answer, row reduce the augmented matrix: $\begin{bmatrix} 1 & -3 &3 \\ 3 & 5 & 2\\ -1 & 7 &5\end{bmatrix} \sim \begin{bmatrix} 1 & -3 &3 \\ 0 & 14 & -7\\ 0 & 4 & 8\end{bmatrix} \sim \begin{bmatrix} 1 & -3 &3 \\ 0 & 1 & 2\\ 0 & 14 & -7\end{bmatrix} \sim \begin{bmatrix} 1 & -3 & 3 \\ 0 & 1 & 2\\ 0 & 0 & -35\end{bmatrix} \tag{3}$
• The third equation, $0 = −35$, shows that the system is inconsistent.
• So $\textbf{c}$ is not in the range of $T$. $\blacksquare$

Shear Transformation

Example 3: Let $A=\begin{bmatrix} 1 & 3 \\ 0 & 1 \end{bmatrix}$. The transformation $T: \mathbb{R}^2 \mapsto \mathbb{R}^2$ defined by $T(\textbf{x})=A\textbf{x}$ is called a shear transformation.

• It can be shown that if $T$ acts on each point in the $2\times 2$ square shown in Fig. 4 below, then the set of images forms the shaded parallelogram.

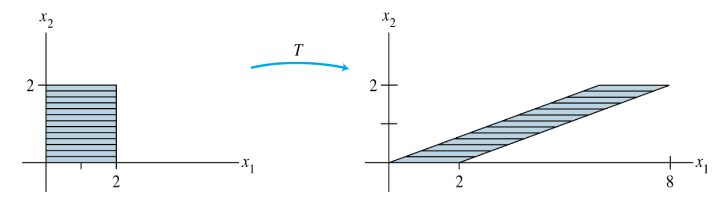
• The key idea is to show that $T$ maps line segments onto line segments and then to check that the corners of the square map onto the vertices of the parallelogram.

• For instance, the image of the point $\textbf{u} =\begin{bmatrix} 0 \\ 2\end{bmatrix}$ is $T(\textbf{u})=A\textbf{u}=\begin{bmatrix} 1 & 3 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} 0 \\ 2\end{bmatrix}=\begin{bmatrix} 6 \\ 2 \end{bmatrix}$, and the image of $\begin{bmatrix} 2 \\ 2\end{bmatrix}$ is $\begin{bmatrix} 1 & 3 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} 2 \\ 2\end{bmatrix}=\begin{bmatrix} 8 \\ 2\end{bmatrix}$.

• $T$ deforms the square as if the top of the square were pushed to the right while the base is held fixed. $\blacksquare$

Definition : A transformation (or mapping) $T$ is linear if:

1. $T(\textbf{u}+\textbf{v})= T(\textbf{u}) + T(\textbf{v})$ for all $\textbf{u},\textbf{v}$ in the domain of $T$;
2. $T(c\textbf{u})= cT(\textbf{u})$ for all scalars $c$ and all $\textbf{u}$ in the domain of $T$.

• Linear transformations preserve the operations of vector addition and scalar multiplication.
• Property (i) says that the result $T(\textbf{u}+\textbf{v})$ of first adding $\textbf{u}$ and $\textbf{v}$ in $\mathbb{R}^n$ and then applying $T$ is the same as first applying $T$ to $\textbf{u}$ and $\textbf{v}$ and then adding $T(\textbf{u})$ and $T(\textbf{v})$ in $\mathbb{R}^m$.

These two properties lead to the following useful facts.

• If $T$ is a linear transformation, then $T(\textbf{0})=\textbf{0} \tag{3}$ and $T(c\textbf{u}+d\textbf{v})=cT(\textbf{u})+dT(\textbf{v}) \tag{4}$ for all vectors $\textbf{u},\textbf{v}$ in the domain of $T$ and all scalar $c,d$.
• Property(3) follows form condition (2) in the definition, because $T(\textbf{0})=T(0\textbf{u})=0T(\textbf{u})=\textbf{0}$.
• Property (4) requires both (1) and (2): $T(c\textbf{u}+d\textbf{v})=T(c\textbf{u})+T(d\textbf{v})=cT(\textbf{u})+dT(\textbf{v})$
• If a transformation satisfies (4) for all $\textbf{u}, \textbf{v}$ and $c$, $d$, it must be linear.
• (Set $c = d = 1$ for preservation of addition, and set for $d = 0$ preservation of scalar multiplication.)
• Repeated application of (4) produces a useful generalization: $T(c_1\textbf{v}_1+\cdots+c_p\textbf{v}_p)=c_1T(\textbf{v}_1)+\cdots+c_pT(\textbf{v}_p) \tag{5}$
• In engineering and physics, (5) is referred to as a superposition principle.
• Think of $\textbf{v}_1+\cdots+\textbf{v}_p$ as signals that go into a system and $T(\textbf{v}_1)+\cdots+T(\textbf{v}_p)$ as the responses of that system to the signals.
• The system satisfies the superposition principle if whenever an input is expressed as a linear combination of such signals, the system’s response is the same linear combination of the responses to the individual signals.

Contraction and Dilation

• Given a scalar $r$, define $T: \mathbb{R}^2 \mapsto \mathbb{R}^2$ by $T(\textbf{x})=r\textbf{x}$.
• $T$ is called a contraction when $0\le r \le 1$ and a dilation when $r>1$.