Logistic Regression¶

Logistic Regression은
이름과 달리, binary classification task를 위한 모델로서
특정 class에 속할 확률을 결과값으로 가짐.(output이 하나의 확률값임).

Label은 일반적으로 1 또는 0 으로 표기하여
특정 class에 속하는 경우 1을 label로 가지고
해당 class에 속하지 않고 다른 class에 속하는 경우 0을 label 값으로 함.

실제로 Logistic Regression에서는
두 class 중 하나를 지정하여 해당 class에 속할 경우를 1로,
아닐 경우를 0으로 지정(label이 해당값으로 설정됨)한다.

즉, Logistic Regression의 출력(예측 class)은 1에 해당하는 class에 속할 확률이 된다.

Logistic Regression의 동작 순서는 다음과 같음.

Regression으로 어떤 score $t$ (=logit score or log odds score )를 구함
해당 score를 logistic function의 입력값으로 넣으면 0~1사이의 확률값 $\hat{p}$이 나옴.
해당 확률로 classification (binary classification)

참고 : Logit의 개념과 이를 통한 Logistic Regression 유도

이 문서는 Logistic Regression을
Bernoulli Distribution에 기반한
Maximum Likelihood Expectation의 관점으로 해석 하여
DL에서의 binary classification model에 대한 이해로
확장해나가는 것을 목표로 함.

다음 그림은 Computational Graph 또는 Single Layer Perceptron (or Dense Layer)로 표현한 Logistic Regression임.

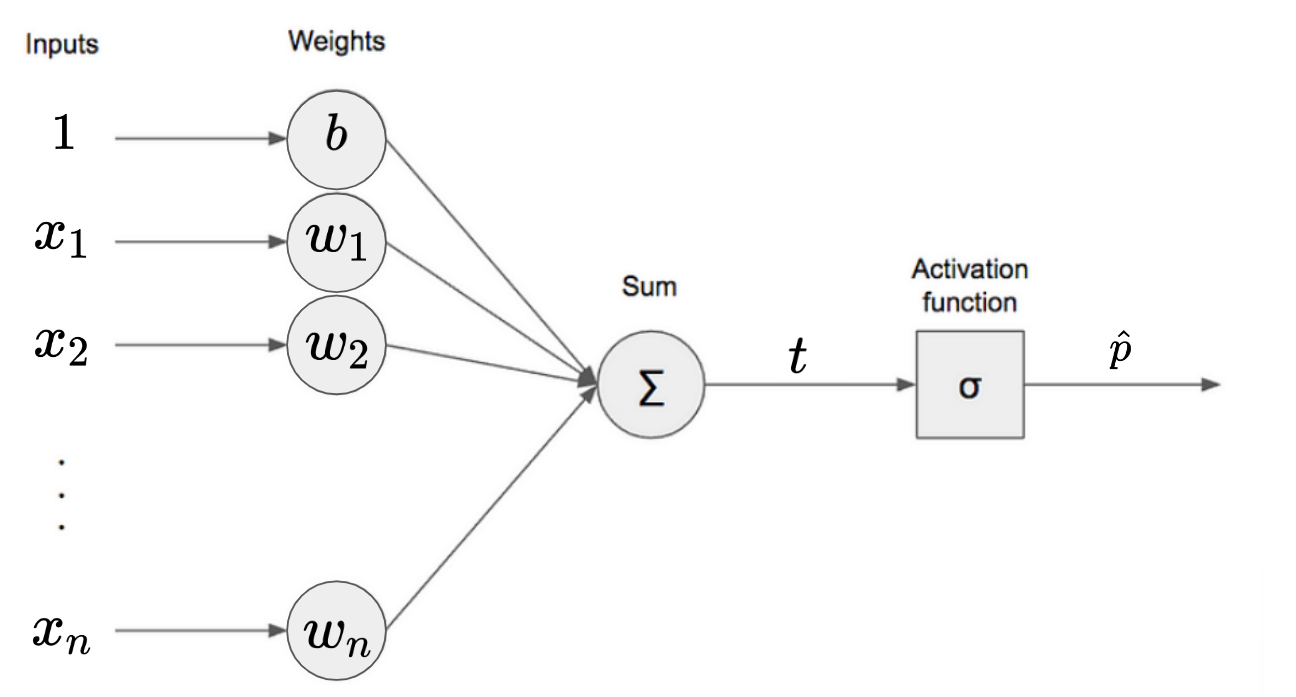
다음은 Logistic Regression의 출력 $\hat{p}$의 수식이다. $$ \hat{p}(\hat{y}=1) = \sigma(t) = \sigma \left( b+\omega_1x_1+\omega_2x_2 +\dots+\omega_n x_n\right) \ \quad \ \hat{p}(\hat{y}=1) = \hat{p} $$

class 1에 속할 확률 $\hat{p}(\hat{y}=1)$이 출력임.
0.5 이상일 경우 class 1에 속한다고 판정하고, 미만일 경우는 class 0에 속한다고 판정.

figure ori.

Binary Classification¶

input $\textbf{x}$가 주어질 경우,
하나의 클래스에 속하는지 안 속하는지를 결정하는 task를 binary classification 이라고 함.

하나의 클래스에 속하는 경우(=1)와 속하지 않는 경우(=-1) 두 개의 클래스ㄹ 가지기 때문에 binary classification 이라고 불림.

ANN 등으로 만들 경우,
output이 숫자 하나로 나오며
이는 class 1에 속할 확률 $\hat{p}$ 에 해당함.

앞서 설명한 Logistic Regression의 경우와 같음.

동시에, 다른 class에 속할 확률은
$\hat{q}=1-\hat{p}$ 이 된다.

해당 task에 대해 label은 $y \in \{0,1\}$로 주어져서
$i$번째 input $\textbf{x}^{(i)}$에 대응하는 label $y^{(i)}$는 0 또는 1 중의 하나가 된다.

$i$번째 sample의 label $y^{(i)}$가 1의 값인 경우, $i$번째 sample이 class 1에 속할 확률이라고 생각할 수 있다.
- 정답은 고정이니 확률이 100%인 1로 기재.
$i$번째 sample의 label $y^{(i)}$가 0의 값인 경우도 역시 $i$번째 sample이 class 1에 속할 확률이라고 생각할 수 있다.
- 정답은 고정이니 확률이 0%인 0으로 기재.
- $i$번째 sample이 class 0 으로 label이 지정된 경우, 해당 sample이 class 1일 확률은 0이 된다.

즉, $i$번째 sample의 label $y^{(i)}$를 class의 index로 봐도 되지만, class 1에 속할 확률이라고 볼 수도 있다.

이는 달리 말하면 binary classifier의 output은
class 1에 속할 확률 이라고 볼 수 있음을 의미한다.

Posterior probability로 살펴본 Binary classification.¶

binary classification model의 output인,
$\hat{y}$가 1일 확률 $\hat{p} = \hat{p}(\hat{y}=1)$ 는
Logistic regression의 경우 다음과 같음.

\[\hat{p}=h_{\boldsymbol{\theta}}(\textbf{x})=\sigma(\textbf{x}^T\boldsymbol{\theta})\]

$h_{\boldsymbol{\theta}}( \cdot )$ : hypothesis의 약자 $h$로 model을 나타내는 function임.
- model의 parameters가 $\boldsymbol{\theta}$임을 아래첨자로 나타냄.
$\hat{p}$ : class 1에 속할 probability를 의미.
- model이 예측한 결과이므로 hat $\hat$이 씌어짐.
- Logistic regression의 output임.
- 일반적인 binary classifier의 output이기도함.
- $\hat{p}(\hat{y}=1)$ 를 줄여서 표현한 것임.
$\sigma( \cdot )$ : Logistic function.

Logistic Regression의 output $\hat{p}$ (class 1에 속할 probability)는
$\textbf{x}$와 $\boldsymbol{\theta}$가 주어졌을 때,
Random variable $\hat{y}$가 1의 값을 가질 확률(probability)이기 때문에

해당 확률이 0.5 이상이며 $\hat{y}=1$이라고 판정하고
아니면 $\hat{y}=0$이라고 판정한다고 볼 수 있음.

이를 다음과 같이 표기할 수 있다.

\[p(y=1 | \textbf{x}) \approx \hat{p}(\hat{y}=1 | \textbf{x}; \boldsymbol{\theta}) = h_{\boldsymbol{\theta}}(\textbf{x})\]

이는 model의 (trainable) parameters $\boldsymbol{\theta}$는

training dataset $\left\{(x^{(i)},y^{(i)})| i=1, \dots, M \right\}$ ($M$은 training dataset에서 sample의 갯수임)에서 model로부터 얻는 일종의 conditional probability distribution $\hat{p}(\hat{y}=1| \textbf{x}; \boldsymbol{\theta})$가
실제 training dataset의 확률분포 $p(y=1 | \textbf{x})$에 가장 비슷 ($\approx$)해지도록 조정되어야 함

을 의미한다.

0 또는 1의 값을 가지는 random variable $\hat{y}$에 대한 probability distribution이
label에 해당하는 random variable $y$의 probability distribution이 일치하도록
model의 parameters $\boldsymbol{\theta}$를 조정하기 위해서는

$y$, $\hat{y}$의 probability distribution을 지정하는 Probability Mass Function을 알아야 함.

Logistic regression model이 정답을 맞출 확률 : Bernoulli Distribution¶

Logistic regression 모델이

$i$번째 sample의 input $\textbf{x}^{(i)}$에 대해
정답 $y^{(i)}$을 맞출 확률 $p$는 다음과 같이 정의할 수 있다.

\[p(y^{(i)}|\textbf{x}^{(i)};\boldsymbol{\theta})=(\hat{p}^{(i)})^{y^{(i)}}(1-\hat{p}^{(i)})^{1-y^{(i)}}\]

$p(y^{(i)}|\textbf{x}^{(i)};\boldsymbol{\theta})$는 주어진 $i$번째 input $\textbf{x}$와 현재 model parameters $\boldsymbol{\theta}$ 하에서 모델이 정답(label) $y^{(i)}$를 출력할 likelihood를 의미함.
$\hat{p}^{(i)}=\sigma({\textbf{x}^{(i)}}^T\boldsymbol{\theta})$ 는 input $\textbf{x}^{(i)}$에 대한 logistic regression의 output으로 class 1에 속할 probability임.
즉, $\hat{p}^{(i)}$는 $\hat{y}=1$이 될 확률이다.

위의 식은
Logistic regression model이 정답을 맞출 확률 $p$가 Bernoulli random variable의 distribution 을 따름 을 보여줌

위의 식은 Bernoulli distribution의 PMF임.

ref. : Bernoulli distribution에 대해서

label $y^{(i)}=0$인 경우: Logistic regression model의 output $\hat{p}$가 0에 가까울수록 정답에 가까운 것이므로
위의 $p$는 1에 가까워지고,
반대인 경우엔 $p$는 0에 가까워지므로
결국, 위의 식 $p$는 model의 결과가 얼마나 정확한지를 의미함.
label $y^{(i)}=1$인 경우: Logistic regression model의 output $\hat{p}$가 1에 가까울수록 정답에 가까운 것이므로
정답에 가까울수록 위의 식 $p$는 1에 가까워진다.
즉, $p$는 model의 결과가 얼마나 정확한지를 의미함.

참고로
Bernoulli random variable 은

0 또는 1을 값으로 가지는

discrete random variable 임.

이는 Binary classification가 Bernoulli trial로 볼 수 있음을 의미함.

달리 말하면 binary classification model이 정답을 맞출 확률은

Bernoulli probability distribution 을 따른다고 볼 수 있음.

위의 $p(\hat{y}|\textbf{x};\boldsymbol{\theta})$를 likelihood로 삼고

(ref. : likelihood (우도))

이를 최대화하는 maximum likelihood expectation (MLE)를 기재하면 다음과 같음.

\[\begin{aligned}\boldsymbol{\theta}&=\underset{\boldsymbol{\theta}}{\text{argmax }} \prod _{i=1}^M p(y^{(i)}|\textbf{x}^{(i)};\boldsymbol{\theta})\\&=\underset{\boldsymbol{\theta}}{\text{argmax }} \prod _{i=1}^M \mathcal{L}(\boldsymbol{\theta}|\textbf{x}^{(i)},y^{(i)})\\&=\underset{\boldsymbol{\theta}}{\text{argmax }} \prod _{i=1}^M (\hat{p}^{(i)})^{y^{(i)}}(1-\hat{p}^{(i)})^{1-y^{(i)}}\end{aligned}\]

$\displaystyle \prod _{i=1}^M p(y^{(i)}|\textbf{x}^{(i)};\boldsymbol{\theta})$가 최대화된다는 것은 Logistic regression model이 정답을 맞출 가능성이 커진다는 것을 의미함.
$\boldsymbol{\theta}$를 조절하면 해당 정답을 맞출 가능성 은 변하며, 각각의 $\boldsymbol{\theta}$에 따른 해당 가능성의 값들을 모두 더할 경우 1이 되진 않음 (물론 값이 클수록 가능성은 커짐) : 때문에 likelihood 라고 부르며 이 부분을 강조하여 likelyhood function $\mathcal{L}$로 표기하기도 함.
likelihood 를 구하는데 사용되는 $\hat{p}=\sigma(\textbf{x}^T\boldsymbol{\theta})$ 는 logistic regression의 output으로 $\hat{y}=1$이 될 확률(class 1에 속할 확률)을 의미함.

이 MLE를 통해 구해진
likelihood를 최대화 하는 parameters $\boldsymbol{\theta}$ 를
가지는 model이 바로 binary classification task에 대한 최적의 model 이 됨.

위의 식의 경우,
각 likelihood들의 joint probability 를 통해

training dataset의 모든 $M$개의 sample들을 고려하여

최적의 parameters $\boldsymbol{\theta}$를 구한다.

단, 각 sample들이 서로의 class를 결정할 때 각 sample간에 독립 적으로 구해진다는 가정에 기반.

MLE의 object function은 utility function으로 최대화가 목적임.

Negative Log-Likelihood¶

MLE는 utility function을 사용하므로 최대화가 목표 이므로,
최소화를 사용하는 Gradient Descent의 loss function으로 이를 사용하기 위해서는
다음과 같은 처리가 필요함.

위의 likelihood에

- 기호를 붙여주면(negation) 된다.

즉, utility function에 -1을 곱하면 loss function이 된다.

그리고 likelihood를 training dataset의 모든 샘플에 대해 적용할 때,

joint probability이기 때문에
각 likelihood를 곱해야 하는데,
이처럼 곱해주는 것($\prod$)보다는
더해나가는게($\sum$) 편하므로
$\log$를 취해주는 경우가 일반적임.

이같은 방식을 가르켜 Negative Log Likelihood 라고 부름.

Negative : loss function으로 삼아 최소화 문제로 변경.
Log : $\prod$ 대신 $\sum$을 사용하기 위해.

이를 통해 얻은 Object function (=loss function) $J$는 다음과 같음.

\[J(\boldsymbol{\theta}) = -\frac{1}{m} \sum_{i=1}^m \left[ y^{(i)}\log \left(\hat{p}^{(i)}\right)+ (1-y^{(i)})\log\left(1-\hat{p}^{(i)}\right)\right]\]

$J(\boldsymbol{\theta})$는 loss function이 parameters $\boldsymbol{\theta}$를 독립변수로 삼는 함수임을 강조한 표기.
이 loss function을 Logistic Loss 또는 Negative Log Loss, Log Loss 라고 부름.

지금까지 살펴본 내용은 다음을 의미함.

binary classification인 logistic regression은 일종의 MLE라고 볼 수 있다.
해당 MLE는 정답을 맞출 확률분포가 Bernoulli Distribution이라는 것을 기반으로 한다.
Likelihood objective function을 Negative Log Likelihood로 바꾸어서 사용한다.

DL에서 binary classification에서 이용하는 cross-entropy 와 위의 Negative Log Likelihood 를 살펴보면 매우 유사함을 알 수 있음.

Cross Entropy란?

참고로 위의 loss function은 linear regression (=logistic activation이 없는 경우)과 달리 closed form solution이 알려져 있지 않음.

Normal equation과 같은 analytic method로 최적의 parameter를 단번에 직접 구할 수 없음.
sigmoid activation의 도입으로 non-linear이며, non-linear의 경우 거의 대부분 쉽게 풀리지 않는다(closed form solution 없음). ==;;

하지만, 다행스럽게도 위의 loss function은 convex function 임.

Gradient Decent를 사용할 경우 global minimum에 해당하는 parameters를 항상 구할 수 있음을 의미함.

Logistic cost function partial derivatives¶

loss function $J(\boldsymbol{\theta})$를 $j$번째 parameter $\theta_j$에 대한 partial derivatives는 다음과 같음.

\[\dfrac{\partial}{\partial \theta_j}J(\boldsymbol{\theta})=\frac{1}{M}\sum_{i=1}^M \left( \color{red}{\sigma \left( \boldsymbol{\theta}^\text{T}\textbf{x}^{(i)}\right) - y^{(i)}}\color{black}\right)\color{blue}{x_j^{(i)}}\]

$M$ : training set에서의 instance 수.
각 instance에 대해,
- prediction error (red)를 구하고
- 여기에 해당하는 input vector의 $j$ feature (blue) $x_j^{(i)}$를 곱하고
이를 training set의 모든 instances에 대해 averaging.

위와 같은 partial derivatives를 통해 gradient $\nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta})$를 구하고,
이를 이용한 Gradient Decent method로 parameters를 구해나가면
Logistic regression의 training이 이루어짐.

참고: Gradient Decent Method (GD)

Logistic Regression 과 ANN : negative log loss vs. MSE for binary classification¶

Logistic Regression은 ANN (or DL)의 관점에서 보면

logistic activation의 single fully connected layer (single layer FCN) 임.
(loss function은 cross-entropy).

앞서 살펴본 negative log likelihood object function은 convex 하기 때문에 global minimum을 구하는게 보장된다. (주의할 건 이는 single layer인 경우에 한정됨.)
단, 여러 layer를 쌓는 경우 convexity는 유지되지 않는다.
- DL에서 convexity가 유지되는 경우는 거의 없다고 봐도 된다. ㅠㅠ
- 하지만 DL로 구해진 solution들은 global minimum이라는 보장은 없으나 실제로 task를 수행하는데 충분한 성능을 보임.

달리 말하면, 이 single layer FCN도
negative log likelihood를 object function으로 삼은 (Bernoulli Distribution에 기반한) MLE의 일종
으로 해석가능함을 의미함.

$\boldsymbol{\theta}$는 실제로 여러 개의 parameters로 구성된 vector 이나 이를 scalar로 단순화하고 logistic regression의 objective function을 parameter에 대해 그리면 convex임을 확인 가능함 (input 도 scalar로 단순화하고 이는 고정시킴).

single fully connected layer 로 구현할 경우
ANN의 loss function을
앞서 말한 cross entropy가 아닌,
regression의 경우처럼 다음과 같은 Mean squared loss MSE로 삼을 수도 있긴 함(가능하지만 권장하진 않음).

\[\text{MSE}=\left(\frac{1}{1+e^{-\sum_{i=1}^{N}\theta_i x_i}}-1\right)^2\]

하지만 MSE를 loss로 사용하는 경우,
아래 그림(red line)에서 보이듯이 MSE는 convexity도 성립하지 못하며,
loss function의 최대값 (기껏해야 1)도 제한되는 단점이 있음을
확인할 수 있다.
(반면에 negative log의 경우 loss function은 최대값이 무한대까지의 범위를 보임)

매우 틀린 오답을 현재 parameters의 모델이 보일 경우, negative log loss는 매우 큰 값을 보이지만,
MSE loss는 그리 큰 값을 보이지 못함.
큰 오차에서는 가급적 큰 loss를 가져야 함.
때문에 MSE의 경우, 오차가 큰 초반 epoch 초반에 weight들이 최적의 값으로 빠르게 변화하지 못하는 단점을 추가적으로 가짐.

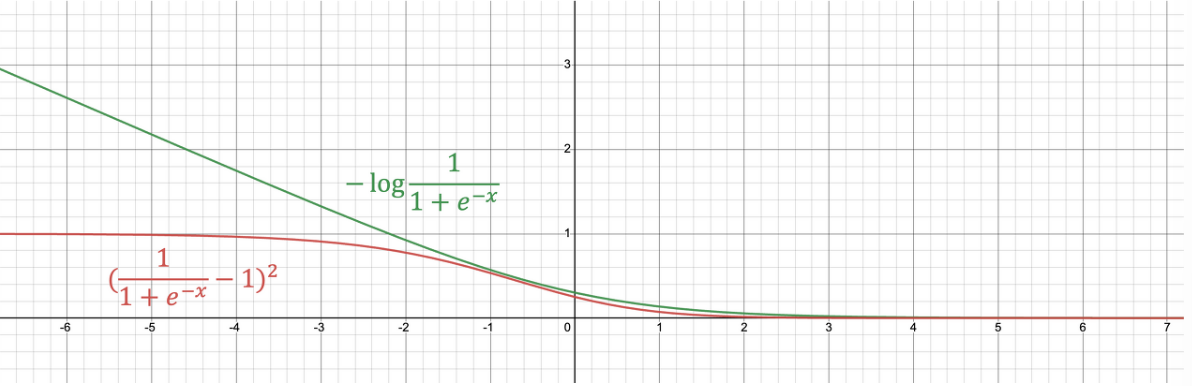
때문에 binary classification task를 수행하는 ANN에서 MSE보다는 cross-entropy를 선호한다.

수학적으로 비교할 경우, weight와 bias에 대한 loss function의 partial derivative를 확인해보면 왜 MSE가 적절치 않은지를 확인할 수 있음.

아래는 MSE의 partial derivative임.
앞서 보였던 logistic regression의 loss (=Cross entropy cost)와 달리
$\color{red}{\sigma^\prime \left(\boldsymbol{\theta}^\text{T}\textbf{x}^{(i)}\right)}$ term이 중간에 추가되어 있는데,
이 sigmoid의 미분 term으로 인해
partial derivative가 작은 값으로 감소하게 되고 이로인해 back-propagation에서 효과적인 training을 하기 어렵게 된다.

\[\begin{aligned}\dfrac{\partial}{\partial \theta_j}J(\boldsymbol{\theta})&=\frac{1}{M}\sum_{i=1}^M \left( {\sigma \left( \boldsymbol{\theta}^\text{T}\textbf{x}^{(i)}\right) - y^{(i)}}\right)\color{red}{\sigma^\prime \left(\boldsymbol{\theta}^\text{T}\textbf{x}^{(i)}\right)}\color{black}{x_j^{(i)}}\\&=\frac{1}{M}\sum_{i=1}^M \left( {\sigma \left( \boldsymbol{\theta}^\text{T}\textbf{x}^{(i)}\right) - y^{(i)}}\right)\color{red}{\sigma \left(\boldsymbol{\theta}^\text{T}\textbf{x}^{(i)}\right)(1-\sigma \left(\boldsymbol{\theta}^\text{T}\textbf{x}^{(i)}\right))}\color{black}{x_j^{(i)}}\end{aligned}\]

logistic의 derivative는 0.25를 max로 가지는 normal distribution의 모양임.
tanh의 경우, logistic보다 큰 derivative를 가지고 있어서 학습에 보다 유리한 것으로 알려짐.

결론적으로 Binary Classification의 경우,
MSE 보다는 cross entropy가 보다 적합한 loss function임.

참고1: derivative of logistic function

참고2: hyperbolic tangent function

Multi-class Classification으로 확장.¶

Logistic regression의 logistic function을 multi-class로 확장하면 softmax function이 된다.

증명 : https://dsaint31.tistory.com/319

이는 binary classification이 logistic function을 activation으로 하던 것을 일반화하여
multi-class classification의 경우
softmax function을 activation으로 삼게 됨을 의미 함.

참고 : softmax function

Logistic Regression이 Beroulli Distribution에 기반한 MLE 였던 것을 multi-class classification으로 일반화하면, Gaussian Distribution에 기반한 MLE가 된다.

즉, Softmax function을 이용한 multi-nomial logistic regression (or softmax regression) 모델은

각 class에서 sample들의 분포가 각각의 class의 중심으로부터 Gaussian Distribution을 따른다.

라고 가정하고 classification이 이루어지는 것이다.

때문에 해당 가정에 맞지 않는 classification task에서는 잘 동작하지 않는다.

비슷하게 MSE를 기반으로 하는 linear regression의 경우,

data가 linear하고 residual error 가 Normal Equation을 따른다.

라는 가정을 기반으로 regression이 수행되기 때문에
해당 가정에 맞지 않는 task에서는 bias가 발생한다.

NFLT (No Free Lunch Theorem)에 의해

Model이 기반하고 있는 가정이 성립하는 경우 해당 model은 좋은 성능을 보이지만,
아닐 경우 더 나쁜 성능을 보일 수 밖에 없다.

참고: No Free Lunch Theorem (NFLT)