Laplacian of Gaussian (LoG)
LoG는 Marr과 Hildreth에 의해 1980년에 제안된 기법.
- Gaussian blurring을 사용하여 noise를 제거(or 완화)시킨 후
- Laplacian을 가하여 edge를 추출.
Laplacian이 edge를 잘 찾아내는 장점을 가지나, noise도 같이 증폭시키는 단점을 가지고 있기 때문에, Laplacian의 장점을 극대화하고 단점을 상쇄하기 위해 제안되었음.
Gaussian Blurring
Gaussian Blurring의 kernel은 다음 수식을 따름.
std인 \(\sigma_x,\sigma_y\)가 커질수록 blurring이 심해짐.
일반적으로는 isotropic이라고 가정하여 \(\sigma=\sigma_x=\sigma_y\)로 처리됨.
\[ G(x,y) = \dfrac{1}{2\pi\sigma_\text{x}\sigma_\text{y}} \exp \left[ -\left( \dfrac{(x-x_o)^2}{2\sigma_\text{x}^2}+\dfrac{(y-y_o)^2}{2\sigma_\text{y}^2}\right)\right] \]
좀 더 단순하게, 앞의 상수 부분을 생략하고 다음으로도 표시하는 경우도 많다.
\[ G(x,y) = \exp \left[ -\left( \dfrac{(x-x_o)^2}{2\sigma_\text{x}^2}+\dfrac{(y-y_o)^2}{2\sigma_\text{y}^2}\right)\right] \]
Laplacian of a Gaussian (LoG)
의료영상을 포함한 영상처리에서 Laplacian은 수평과 수직방향의 2차 미분 에 해당함(Taylor series expansion 으로 approximation이 유도됨)
\[ \nabla^2 f(x,y)=\frac{\partial^2}{\partial x^2}f(x,y)+\frac{\partial^2}{\partial y^2}f(x,y) \]
Log는
- Gaussian filter를 input image \(f\)에 가해주고(convolution)
- 이후에 Laplacian을 가해줌.
좀더 수식에서 중요한 부분에 집중하기 위해 \(x_o=y_o=0\)으로 처리하여 전개하면 다음과 같음.
\[ \begin{aligned}\nabla^2G(x,y)=&\frac{\partial^2}{\partial x^2} G(x,y)+\frac{\partial^2}{\partial y^2} G(x,y)\\=&\frac{\partial}{\partial x}\left[\frac{-x}{\sigma_x^2} \text{exp} \left( -\left( \dfrac{x^2}{2\sigma_\text{x}^2}+\dfrac{y^2}{2\sigma_\text{y}^2}\right)\right)\right]\\&+\frac{\partial}{\partial y}\left[\frac{-y}{\sigma_y^2} \text{exp} \left( -\left( \dfrac{x^2}{2\sigma_\text{x}^2}+\dfrac{y^2}{2\sigma_\text{y}^2}\right)\right)\right]\\=&\left[\frac{x^2}{\sigma_x^4}-\frac{1}{\sigma_x^2} \right] \text{exp} \left(-\left( \dfrac{x^2}{2\sigma_\text{x}^2}+\dfrac{y^2}{2\sigma_\text{y}^2}\right)\right)\\&+\left[\frac{y^2}{\sigma_y^4}-\frac{1}{\sigma_y^2} \right] \text{exp} \left(-\left( \dfrac{x^2}{2\sigma_\text{x}^2}+\dfrac{y^2}{2\sigma_\text{y}^2}\right)\right)\end{aligned} \]
Gaussian blurring처럼 isotropic이라고 가정하면 다음과 같이 좀 더 간단히 정리됨.
\[ \begin{aligned}\nabla^2G(x,y)&=\frac{1}{\pi\sigma^4}\left[\frac{x^2+y^2-2\sigma^2}{2\sigma^2}\right]\text{exp}\left(-\frac{x^2+y^2}{2\sigma^2}\right)\\&=-\frac{1}{\pi \sigma^4}\left[1-\frac{x^2+y^2}{2\sigma^2}\right]\text{exp}\left(-\frac{x^2+y^2}{2\sigma^2}\right)\end{aligned} \]
Gaussian blurring처럼 앞의 normalization factor \(\frac{1}{2\pi \sigma^2}\)를 생략한 형태도 많이 사용됨.
\[ \nabla^2G(x,y)=\left[\frac{x^2+y^2-2\sigma^2}{\sigma^2}\right]\text{exp}\left(-\frac{x^2+y^2}{2\sigma^2}\right) \]
3-D plot and Kernel
아래 그림에서 보이듯이 멕시코 전통 모자를 뒤집어놓은 것처럼 보여서 LoG 연산자는 Mexican hat 연산자 라고도 불림.
여기에 -기호를 씌운 다음의 형태(negative LoG)도 많이 사용됨.
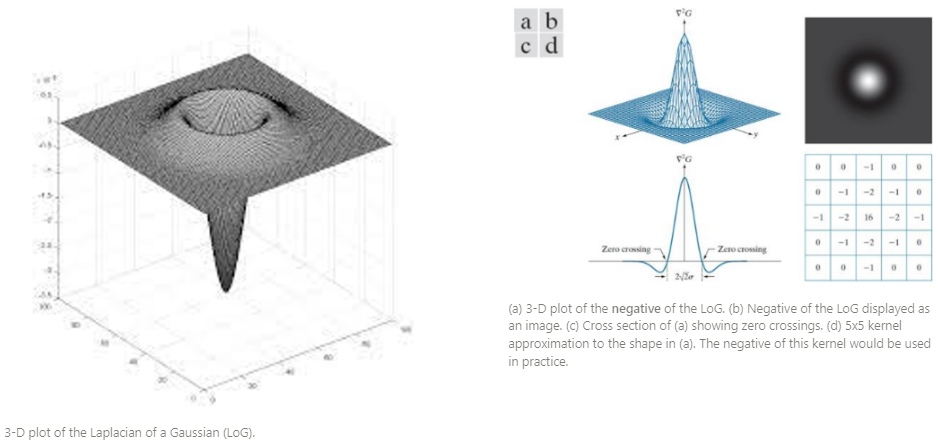
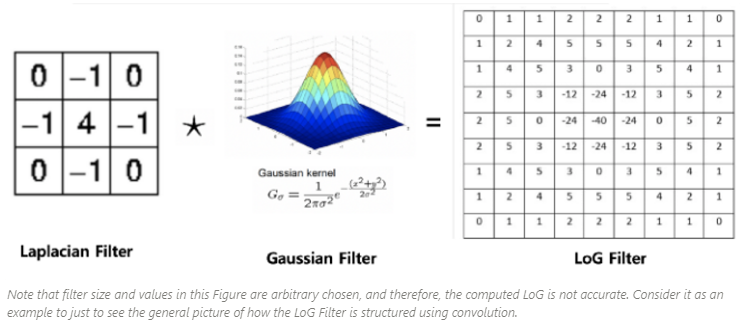
LoG는 frequency domain으로 생각하면,
- Laplacian Kernel과
- Gaussian Blurring Kernel을 곱한 것 이
바로 LoG의 Kernel 이 된다. (spatial domain의 convolution이 freq. domain에서는 곱하기가 됨)
다음은 \(9\times 9\) LoG kernel을 다음 그림에서 보여준다.
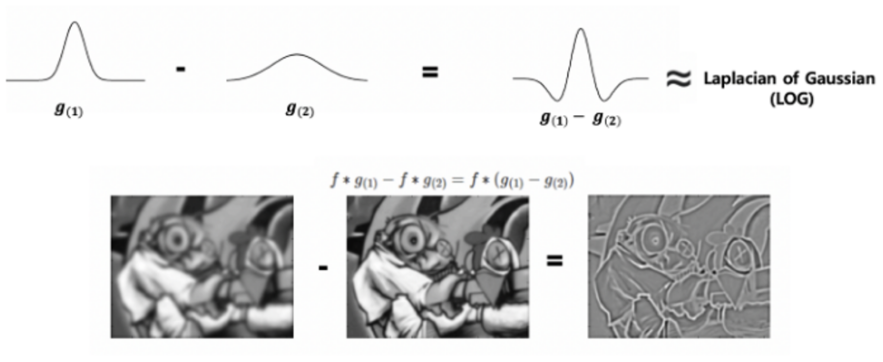
Difference of Gaussian (DoG)
1980년 Marr와 Hildreth에 의해 제안된 LoG의 경우,
- 계산량 측면에서 불리한 점들이 있어서 직접 사용되기 보다는
LoG의 approximation들이 보다 많이 사용 된다.
가장 대표적인 LoG의 approximation이 바로 Difference of Gaussian (DoG)이며 다음 그림이 DoG를 잘 설명해준다.
 RWTH Aachen, computer vision group
RWTH Aachen, computer vision group
- 주의할 점은 Gaussian filter \(g(1), g(2)\)가 각기 다른 \(\sigma\)를 가진다는 점임.
- SIFT등에서도 일반적으로 LoG가 아닌 DoG를 사용한다.
수식으로 DoG가 어떻게 LoG의 approximation이 되는지는 다음 URL을 참고하라.
References


