Skip to content

Harris and Stephen Corner Detection (1988)

C.Harris and M.Stephens. A Combined Corner and Edge Detector.
Proceedings of the 4th Alvey Vision Conference: pages 147-151, 1988.

특정 point가 corner, edge인지 여부를 식별할 수 있는 방법 :

  • local feature detection의 기법으로 많이 애용됨: corner는 local feature로 사용하기 좋은 key point에 해당함.
  • SIFT Feature Detector 에서 사용된다.
  • Gradient에 기반한 Structure Tensor를 사용하는 대표적인 Corner Detection알고리즘임.
  • scale에 대해 취약한 단점이 있어서 SIFT에서는 이를 보완하여 사용한다.

하지만, Harris and Stephen이 제안한 방법은

  • mathematical approach로서
  • SIFT 를 포함한 여러 방법의 기반이 되어줌.

참고로 Harris Corner Detector도 Moravec의 SSD에 기반함.

  • Moravec이 제안한 Moravec Feature Point Detector (1977)에서 사용하고 있는
  • (Weighted) Sum of Squared Difference (SSD 또는 Difference 대신 Error를 써서 SSE 라고도 함)를 사용함.

(Weighted) Sum of Squared Difference (SSD)

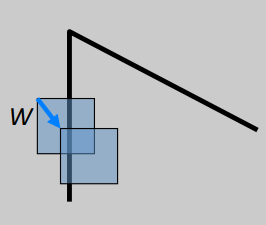
특정 point, \((x_i,y_i)\)에서 \((\Delta x, \Delta y)\) 만큼 특정 크기의 local window, \(W\)를 이동시켜서 (Weighted) Sum of Squared Difference (SSD), \(E\)를 계산한다.

\[E(\Delta x, \Delta y) = \sum_{(x, y) \in W} W( x, y) \left[ I(x+\Delta x, y+\Delta y)-I(x, y) \right]^2\]

where

  • \(W(x, y)\) : Gaussian kernel 또는 uniform rectangular kernel가 사용됨.
    • 일종의 가중치(weight)임.
    • 이 문서에서는 1로 채워진 rectangular kernel이라고 가정함(for simplicity).
    • Window function이라고도 불림.
  • \(I(~)\) : 입력영상의 값.
  • \((x_i, y_i) \in W\) : \((x_i, y_i)\)는 일반적으로 kernel \(W\)의 anchor (가장 가운데)에 해당함.

특정 point \((x_i, y_i)\)에서 여러 방향의 SSD를 계산하여

  • 거의 모든 방향으로 증가하면 corner이고,
  • 변화가 없으면 flat region이라고 생각할 수 있음.

Moravec Feature Point Detector (1977) 의 경우,
위,아래,왼쪽,오른쪽으로 윈도우를 이동시켜서 각각의 SSD들을 구하고
이들 중 최소값을 cornerness 로 규정했음.

참고자료:

Approximation by Taylor Series Expansion

Taylor series expansion를 통해 \(I(x+\Delta x, y+\Delta y)\)를 근사하면 다음과 같음.

\[ \begin{aligned}f(x+\Delta x)&\approx f(x)+\frac{df(x)}{dx}\Delta x \\I(x+\Delta x, y+\Delta y)&\approx I(x, y) +\dfrac{\partial I(x,y)}{\partial x} \Delta x +\dfrac{\partial I(x,y)}{\partial y} \Delta y\end{aligned} \]
  • 위 식은 Taylor series expansion에서 1차 미분까지만 사용하여 approximation을 수행함.

이를 SSD \(E\)에 대입하면 다음과 같은 approximation을 얻게 됨.

\[\begin{aligned}E(\Delta x,\Delta y) &= \sum_{(x,y) \in W} W(x,y) \left[ I(x+\Delta x, y+\Delta y)-I(x, y) \right]^2\\&\approx\sum_{(x,y) \in W} W(x,y)\left[ \left( \dfrac{\partial I(x,y)}{\partial x} \Delta x \right)^2 + \left( \dfrac{\partial I(x,y)}{\partial y} \Delta y \right)^2 +2 \dfrac{\partial I(x,y)}{\partial x}\dfrac{\partial I(x,y)}{\partial y} \Delta x \Delta y\right]\end{aligned}\]

Quadratic Form Approximation

위 식은 다음과 같은 Quadratic form으로 표현이 가능함.

\[E(\Delta x,\Delta y) \approx \displaystyle \sum_{(x,y) \in W}W(x,y) \left(\begin{bmatrix} \Delta x & \Delta y \end{bmatrix} \begin{bmatrix} (\frac{\partial I}{\partial x})^2 & \frac{\partial I}{\partial x}\frac{\partial I}{\partial y}\\ \frac{\partial I}{\partial x}\frac{\partial I}{\partial y} & (\frac{\partial I}{\partial y})^2 \end{bmatrix} \begin{bmatrix} \Delta x\\ \Delta y \end{bmatrix}\right)\]

이를 전개하면 다음이 성립.

\[\begin{aligned}E(\Delta x,\Delta y) &\approx \displaystyle \begin{bmatrix} \Delta x & \Delta y \end{bmatrix} \left(\sum_{(x,y) \in W}W(x,y)\begin{bmatrix} (\frac{\partial I}{\partial x})^2 & \frac{\partial I}{\partial x}\frac{\partial I}{\partial y}\\ \frac{\partial I}{\partial x}\frac{\partial I}{\partial y} & (\frac{\partial I}{\partial y})^2 \end{bmatrix} \right) \begin{bmatrix} \Delta x\\ \Delta y \end{bmatrix} \\&= \displaystyle \begin{bmatrix} \Delta x & \Delta y \end{bmatrix} \begin{bmatrix} W\circledast (\frac{\partial I}{\partial x})^2 & W\circledast \frac{\partial I}{\partial x}\frac{\partial I}{\partial y}\\ W\circledast \frac{\partial I}{\partial x}\frac{\partial I}{\partial y} & W\circledast (\frac{\partial I}{\partial y})^2 \end{bmatrix} \begin{bmatrix} \Delta x\\ \Delta y \end{bmatrix}\\&= \displaystyle \begin{bmatrix} \Delta x & \Delta y \end{bmatrix} \begin{bmatrix} h_{xx} & h_{xy} \\h_{xy} & h_{yy} \end{bmatrix} \begin{bmatrix} \Delta x\\ \Delta y \end{bmatrix}\\&=\textbf{u}^\top H\textbf{u}\end{aligned}\]

where

  • \(\textbf{u}\)를 보통 unit vector로 처리한다.
    • 길이 1씩만 shift. (\(\Delta x = \Delta y = 1\))
  • \(\Delta x, \Delta y\)에 상관없이 전체 이미지 각 pixel에서 matrix \(H\)는 계산이 가능함.
    • \(H\)는 \(2 \times 2\) matrix임.
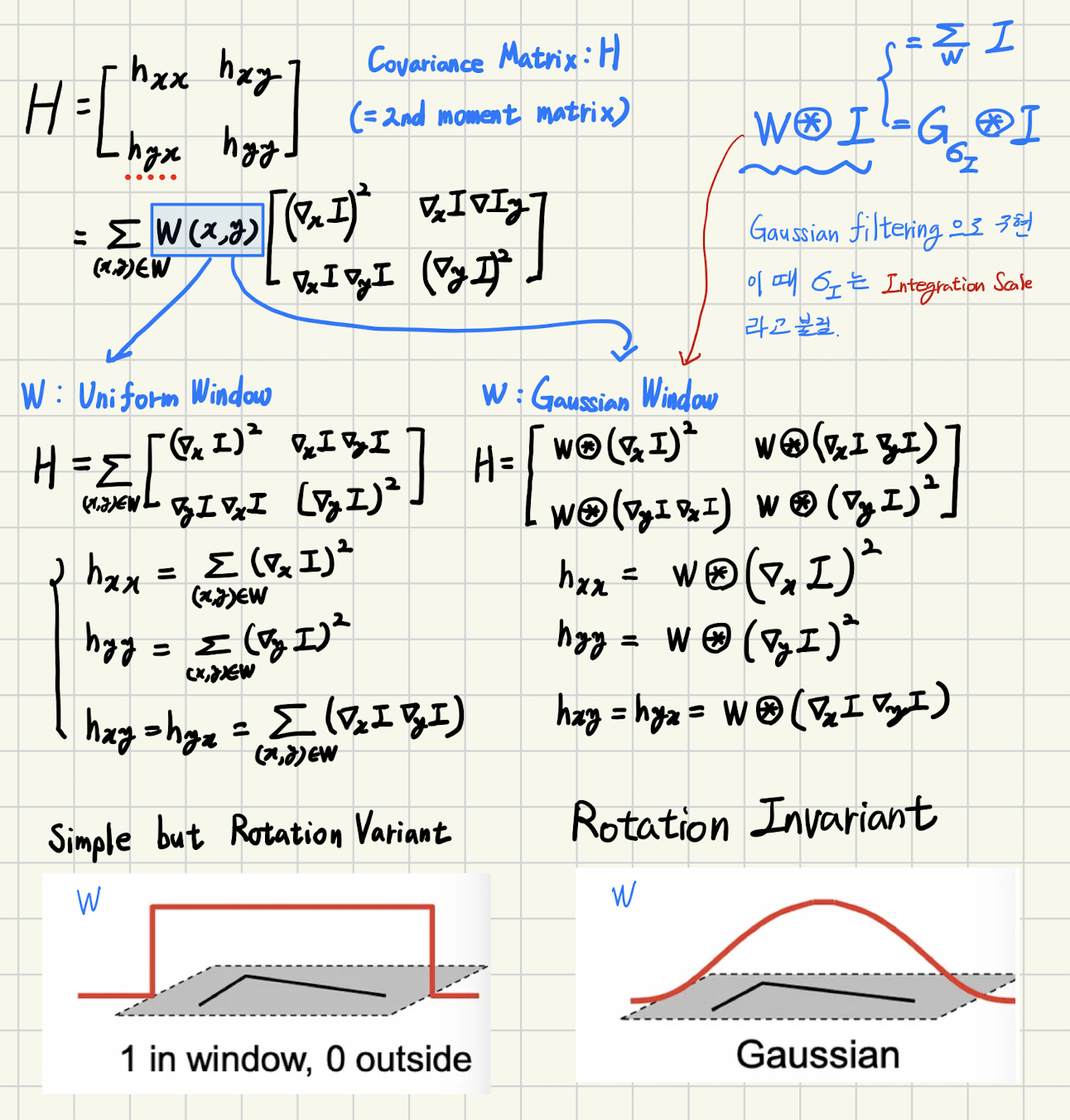
    • \(H\)는 Covariance Matrix (or 2nd moment matrix)이며 \(M\)으로 표기되는 경우도 많음.
  • 편미분은 일종의 difference (차분) 으로 근사됨
    • 수식으로는 다음이 성립: \(\frac{\partial I}{\partial x}= \nabla_x I = I_x\)
    • 해당 축에 대한 difference (차분)을 통해 얻어짐.
    • difference를 수행하기 전에 Gaussian Blurring을 하는 경우가 많고,
    • 이 때의 \(\sigma_d\)를 가르켜 difference scale이라고 부름.
    • 미분을 차분으로 근사관련해서 다음을 참고: 미분과 차분
  • \(W\circledast\) 는 window 내의 대응하는 weights 를 이용하는 weighted sum임.
    • Uniform인 경우가 가장 단순하지만, 성능은 좋지 못함 (Not Rotation Invariant).
    • Gaussian Window가 흔히 사용됨.
    • weighted sum이므로 결국 \(H\)는 \(2 \times 2\) matrix가 됨.

\(W\)를 어떤 것을 사용하는냐에 따라 성능의 차이가 있음.

  • local feature로서 코너를 검출하기 위해선 Rotation Invariant 해야함.
  • 때문에 Gaussian Window가 Uniform Window 보다 선호됨.

Structure Tensor and Curvature

여기서, quadratic form의

  • 가운데 matrix \(H\)를 가르켜 Structure Tensor라고 부름.
    • PCA등의 Covariance Matrix 와 비슷.
    • 뒤에 다룰 Hessian과도 비슷함.
  • \(H\)는 항상 symmetric이므로 eigen decomposition이 가능 (정확히는 orthogonal diagonalization) 함.

eigen decomposition이나 orthogonal diagonalization 등의 좀 더 자세한 내용은 다음 URL 참고:

참고

가운데 Structure Tensor \(H\)는 Auto-correlation matrix 또는 2nd moment matrix라고도 불림.
\(\frac{1}{2}I^2\)의 Hessian의 approximation (Taylor expansion에서 2차항을 무시한 approximation)으로도 볼 수 있음.

위의 \(2 \times 2\) Covariance matrix \(H\)의 경우,

  • diagonalization (or eigen decomposition)을 통해
  • 2개의 eigen value와 서로 orthonormal한 eigenvector 2개를 얻을 수 있음.
\[H=Q\Lambda Q^{-1}=Q\Lambda Q^\top\]

where

  • \(Q\)는 eigen vector들을 column으로 가지는 matrix.
    • Structure Tensor가 항상 symmetric임.
    • Symmetric matrix를 orthogonal diagonalization 할 경우,
    • 각 column 에 해당하는 eigen vector들은 mutually orthogonal 임.
    • 때문에 \(Q\)는 orthogonal matrix임: \(Q^{-1} = Q^\top\).
  • \(\Lambda\)는 eigen value들이 main diagonal에 위치하는 diagonal matrix임.
  • 결국 x축, y축이 아닌,
    • \(E\)가 이루는 quadratic form의 horizontal plane (or horizontal slice) 들에서 이루는
    • ellipse의 equation의 primal axis와 secondary axis를 basis로 하는 change basis가 처리되고
    • 각 길이에 해당하는 곱이 이루어진 이후 다시 x축, y축으로 change of basis가 이루어지게 된다.
  • ellipse는 \(E\)에서 같은 값을 가지는 등고선이라고 볼 수 있으므로,
    • 장축에 해당하는 방향 (\(\lambda_\text{min}\)에 대응)으로는 SSD의 변화가 크지 않고
    • 단축에 해당하는 방향 (\(\lambda_\text{max}\)에 대응)으로는 SSD의 변화가 큼.
  • \(Q\)와 \(Q^\top\) 는 일종의 회전변환 으로 SSE의 변화율이 최대인 축과 이에 직교하는 축으로 basis를 변환시키고, 이를 다시 원래 축으로 돌리는 역할을 수행함.

다음 내용은 \(H\)의 diagonalization이 surface \(E\)에서의 horizontal slice에서의 ellipse와의 관계를 보여준다.

위의 식에서 \(I_{xx}\)는 앞서의 \(h_{xx}\)와 같으며, \(I_x^2\)으로도 표기될 수 있다.

  • 이는 x-axis를 따라 구해진 1st order derivative의 제곱에 해당한다.

이들 중

  • eigen vector 는 각각 \(^{(1)}\)curvature가 최대인 방향과 \(^{(2)}\)해당 방향에 직교한 방향을 가르키며,
  • eigen value 는 이들 축(axis)에서 SSD의 curvature(곡률) 크기에 비례함.

다음은 이를 잘 보여줌.

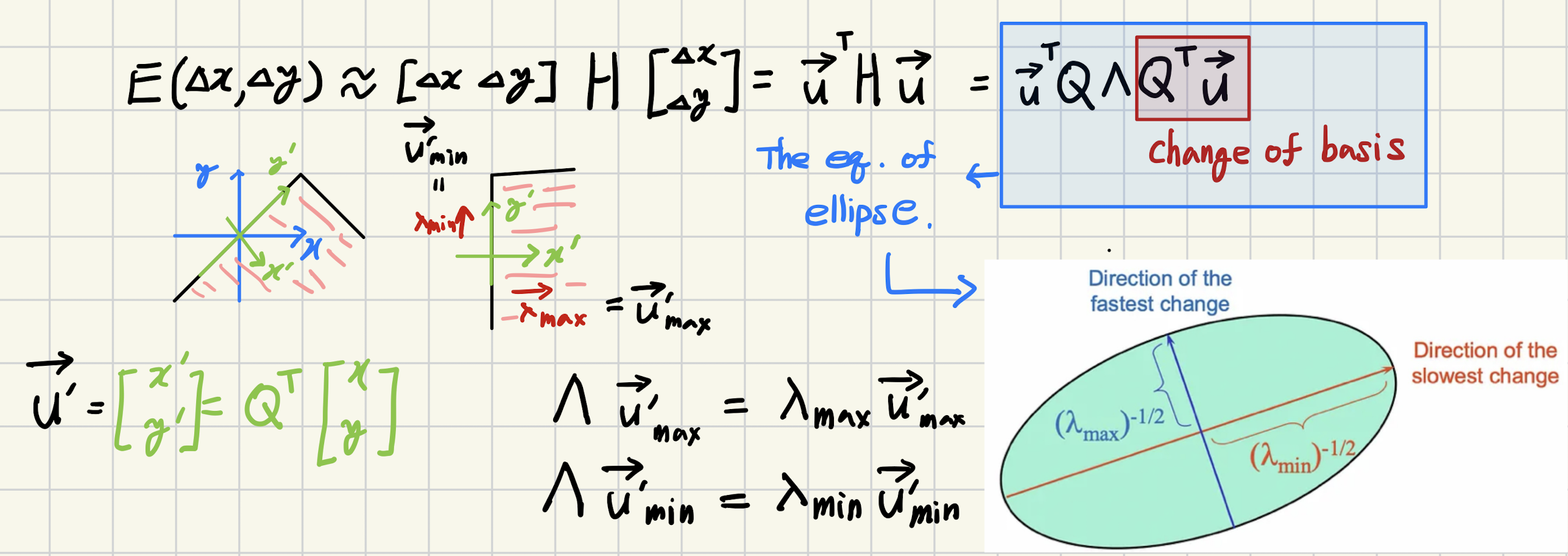
  • \(Q^\top\)를 통해 SSD의 변화가 가장 심한 축과 이에 직교하는 축으로 change of basis가 이루어져 \(\mathbf{u}=\begin{bmatrix} x' & y' \end{bmatrix}^\top\) 로 회전이동이 이루어짐.
  • \(\lambda_\text{max}\)와 \(\lambda_\text{min}\) 은 SSD가 가장 크게 변하는 축과, 이에 직교하는 축에서의 SSD의 변화의 정도를 의미함.

다음은 \(Q, Q^\top\) 가 축을 바꿔주는 일종의 회전행렬이라는 점에 대한 이해를 위한 change of basis를 나타냄.

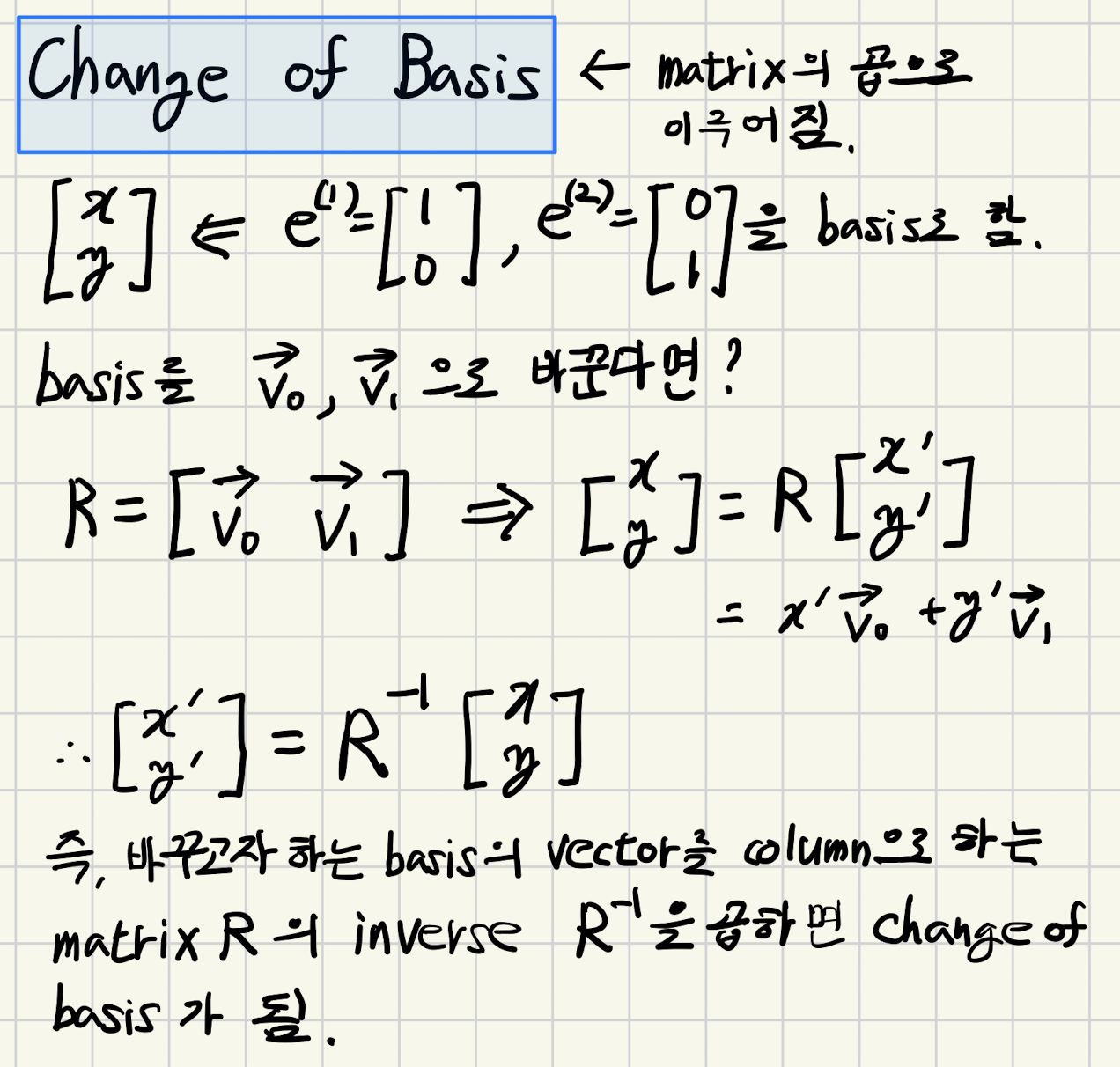
  • \(R^{-1}\)이 앞서의 \(Q^\top (=Q^{-1})\)에 해당함.
  • 즉, eigenvalue에 해당하는 축으로 basis를 바꾸는 것에 해당함.

다음은 ellipse의 equation을 quadratic form으로 표현되는 점을 나타내어 eigen decomposition으로 근사를 이해할 수 있게 해줌.

\(E\)는 SSD를 의미하며

  • 모든 방향에 대해 pixel값이 다른 경우인 corner에선, SSD가 커지므로
  • 이에 대한 locally approximation 인 quadratic form 의
  • Covariance matrix \(H\)의 eigen vector와 eigen value들을 통해
  • edge인지 corner인지를 가늠할 수 있음을 의미함.

\(E\)에서의 curvature는 주변 pixel간의 변화가 짧은 공간에서 급격히 이루어질수록 커짐.

이를 정리하면 다음과 같음(eigen vector의 방향에서 pixel value의 변화량이 eigen value에 해당하며 이는 해당 방향으로의 curvature임)

  • \(\lambda_0 \gg \lambda_1 \text{ or } \lambda_0 \ll \lambda_1\) : edge
  • \(\lambda_0,\lambda_1\)이 둘 다 큰 값이며, 큰 차이가 없음. : corner
  • \(\lambda_0,\lambda_1\)이 둘 다 작은 값이며, 큰 차이가 없음. : flat region

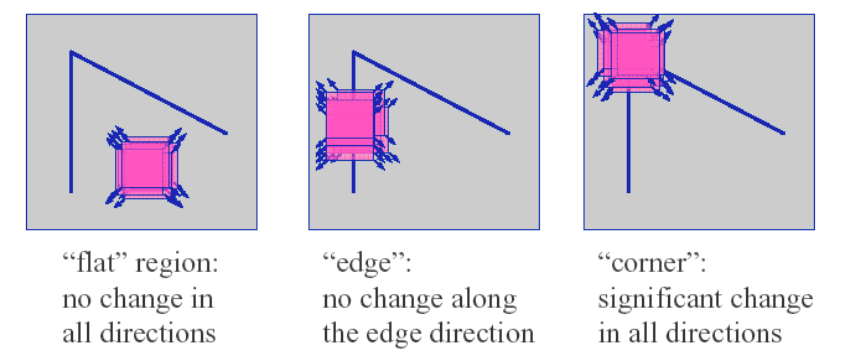
위 그림은 Computer Vision with Python 3, Sauyrabh Kapur, Packt에서 발췌한 것으로 위의 정리를 잘 나타내줌.

타원에서 장축과 단축에 대해,

Structure Tensor 에 대한 eigenvalue에서

  • 큰 값에 해당하는 축이 단축으로,
    • E의 등고선형태 표현인 2D 타원의 곡률이 작으나
    • SSD의 변화에 해당하는 곡률 (=\(E\)의 곡률)은 큼.
  • 작은 값에 해당하는 축이 장축이고
    • E의 등고선형태 표현인 2D 타원의 곡률이 크지만
    • SSD의 변화에 해당하는 곡률 (=\(E\)의 곡률)은 작음.

Hessian 도 eigenvalue를 통해 corner와 edge를 검출할 수 있으면, Edge Detection Response Function에서만 차이를 보임.

Corner Response Function: Determinant와 Trace를 이용.

위의 Structure Tensor의 determinant와 trace의 값을 이용하면 다음과 같은 수식을 얻을 수 있으며,
이를 Harris corner operator라고 부름.
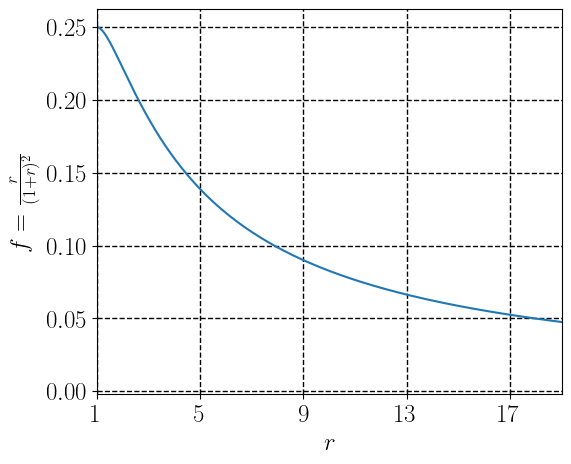
\(\frac{1}{f}\)를 parallel resistor라고도 부른다.(편의를 위해 \(\lambda_0 \ge \lambda_1\)를 가정. → \(r \ge 1\))

\[\begin{aligned}f&=\frac{\lambda_0 \lambda_1}{(\lambda_0+\lambda_1)^2}\\&=\frac{\text{Det}(H)}{(\text{Tr}(H))^2}\\&=\frac{r\lambda_1^2}{ (r\lambda_1+\lambda_1)^2 }\quad \leftarrow \lambda_0=r\lambda_1\\&=\frac{r\lambda_1^2}{\lambda_1^2(r+1)^2}\\&=\frac{r}{(r+1)^2}\end{aligned}\]

즉, \(\lambda_0 = \lambda_1\) 인 경우(\(r= 1.0\))일 때, 가장 큰 값(\(f=1/4\))을 가짐.

  • 이 경우, \(f\)의 값이 큰 경우는 corner 혹은 flat region임.
  • 즉, \(\lambda_0, \lambda_1\)이 일정값 이상이면서 \(f\)가 큰 값을 가지면 corner임.

위의 Harris operator에 대한 다른 대안으로는 Noble(1989) 및 Szeliski(2005)가 제시한 방식이 있다.

Szeliski의 방법은

  • Harris와 Stephens가 1988년 제안한 방법과 같이 Covariance matrix(or 2nd moment matrix)를 이용하지만
  • corner response function 만 차이가 있음.

Szeliski의 방식을 정확히 기재하면 다음과 같음.

\[f=\frac{\text{Det}(H)}{\text{Tr}(H)+\epsilon}\]

보다 자세한 건 다음을 참고할 것:
M.Brown, R.Szeliski, and S. Winder, Multi-image matching using multi-scale oriented patches,in IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR),vol.1, IEEE, 2005, pp.510–517

Harris corner detector의 또 다른 대안인 Shi-Tomasi operator (1994)의 경우,

  • \(\text{cornerness}=\min(\lambda_0,\lambda_1)\)로 정의되며,
  • 최소 eigen value의 크기가 크면 corner로 판정한다.
  • (Harris operator 와 큰 차이는 없으나 robustness가 조금 떨어진다고 알려져 있음)

characteristic equation \(\text{det}(H-\lambda I)=0\) 으로부터 유도되어 다음의 등식으로 cornerness가 구해짐.

\[\lambda_1 = \frac{1}{2}\left( (h_{xx}+h_{yy})-\sqrt{(h_{xx}-h_{yy})^2+4(h_{xy})^2}\right)\]
  • \(\lambda_0 \ge \lambda_1\)로 sorting 을 시켰다고 가정함.
  • \(I\) 는 Identity Matrix 임.

다음 그림은 왼쪽 상단의 \(I\)에 대한 eigen value들을 보여줌.
edge에서 \(\lambda_\text{max}\)가 매우 큰 값들을 가짐을 확인 가능하며,corner에서 \(\lambda_\text{min}\)이 큰 값들을 가짐을 확인할 수 있음.

위 그림의 중단과 하단은 Harris operator와 Shi-Tomasi 간의 차이점을 보여줌.

Harris & Stephens (1988)의 경우,

  • 실제로는 위의 Harris corner operator가 아닌
  • 다음의 corner response function을 사용한다. (큰 값을 가질수록 corner에 해당함)
\[\begin{aligned}f &=\text{det}(H)-\alpha(\text{Tr}(H))^2 \quad \text{ where }\alpha=1/r=0.1 \\ &=\color{red}{\lambda_0\lambda_1-\alpha(\lambda_0+\lambda_1)^2} \quad \leftarrow \text{uniform window} \\ &=h_{xx}h_{yy}-(h_{xy})^2-\alpha(h_{xx}+h_{yy})^2 \\ &=g_{\sigma_I}(I_{x}^2)g_{\sigma_I}(I_{y}^2)-g_{\sigma_I}(I_{x}I_{y})^2-\alpha \{g_{\sigma_I}(I_x^2)+g_{\sigma_I}(I_y^2)\}^2\\ &\quad \uparrow \text{Gaussian Window with Integration Scale}(\sigma_I)\end{aligned}\]

where

  • \(\alpha\)는 보통 0.04에서 0.1 (or 0.06)로 잡음. (Harris operator에 대응함)

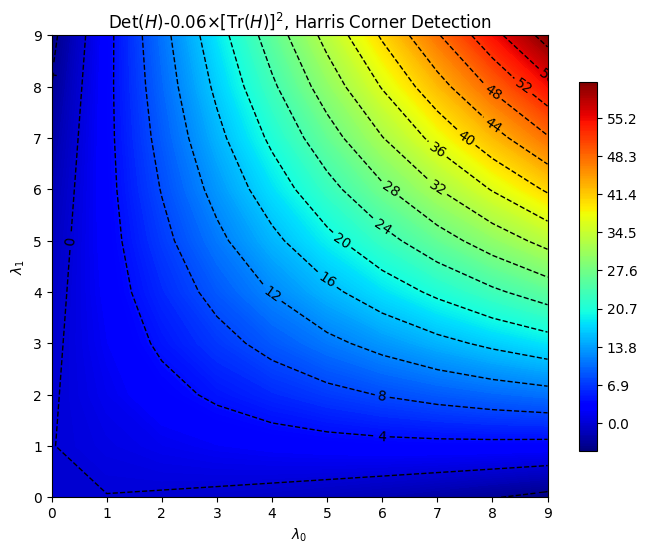
위 그림에서 upper-left와 lower-right는 edge에 해당하고, lower-left는 flat region, upper-right가 바로 corner임. 즉 Harris & Stephens의 \(f\)가 클수록 corner에 해당함.

Hessian 으로 대체

Harris & Stephen Corner Detector 에서 Structure Tensor를 사용하는 부분을,
Hessian로 대체해도 Corner 및 Edge 검출이 가능함.
(Hessian을 사용한 Frangi Filter는 edge detection에 초점을 두고 있음.)

  • Structure 대신에 Hessian Matrix를 사용하여
  • corner 나 edge를 검출 가능함: Hessian Laplace Detector, SURF 등등.

참고: Hessian: Summary

이 경우, Corner Response Function은 다음과 같음.

\[R_\text{Hessian} = det[\text{Hessian}] = I_{xx} I_{yy} - I_{xy}^2\]
  • \(I_{xx}\)는 x축으로 2차 미분한 것으로
  • Hessian 은 2nd derivative로 구성되는 것을 기억할 것.

SURF (Speed-Up Robust Feature)에서 Hessian을 이용함.
SIFT (Scale Invariant Feature Transform)은 Structure Tensor 사용

Implementation

실제 구현은 다음과 같은 순서로 처리가 이루어지도록 구현됨.

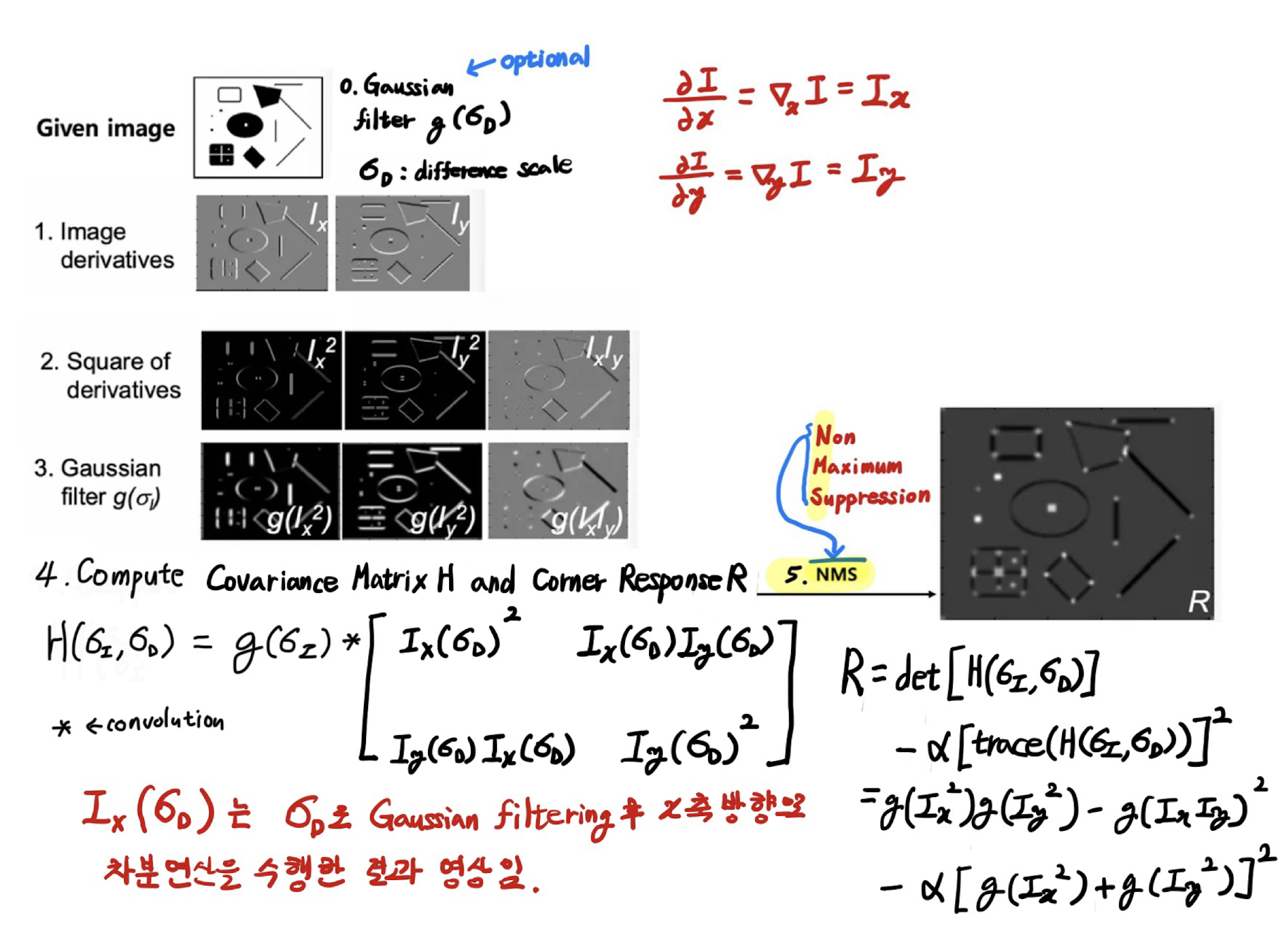
  • difference 대신에 Sobel Filter로 사용하여 구현된다.
  • Sobel Filter를 구현하기 전에 Difference Scale을 std로 가지는 Gaussian Blurring이 이루어짐.
  • 일반적으로 \(\sigma_I > \sigma_D\)임.

Limitation

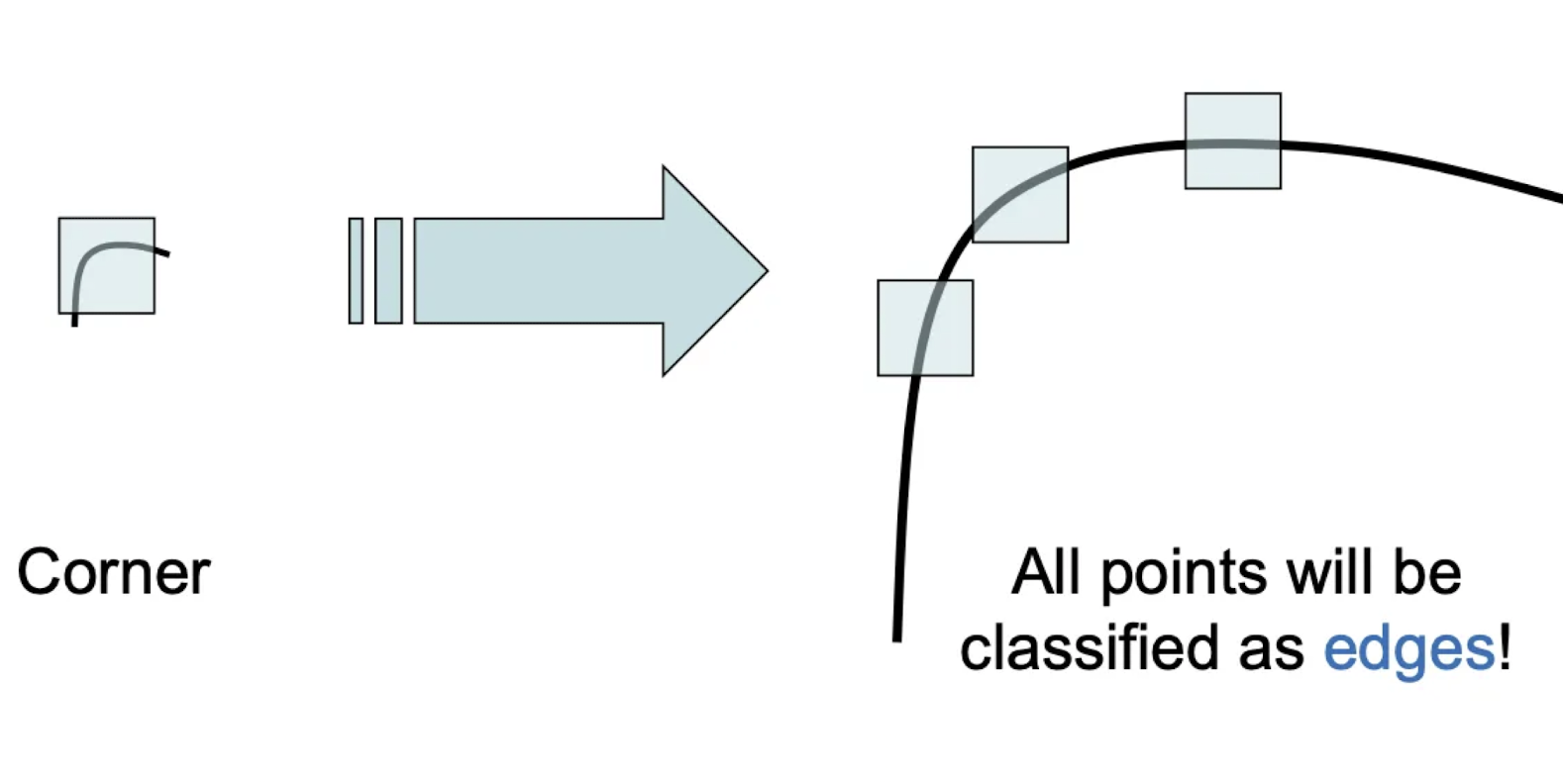
Harris Corner Detection은 Rotation에 대해선 invariant하지만, Scale에 대해선 그렇지 못함.

SSD를 구할 때 사용하는 window의 크기가 고정되기 때문에 image scale variant할 수 밖에 없음.

References