Adder¶

이 문서에서는 gate들로 adder를 구현하는 것을 보여줌.

Half Adder¶

2개의 bit를 입력으로 하여 addition을 수행함.

이전 자리에서 넘어오는 carry에 대한 고려가 없음
때문에 half adder라고 불림.

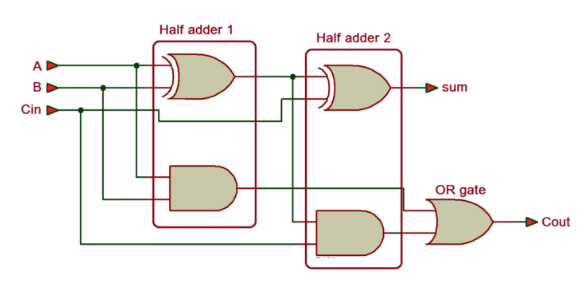
Full Adder¶

2개의 bit와 이전 자리에서 넘어오는 carry를 고려한 addition을 수행함.

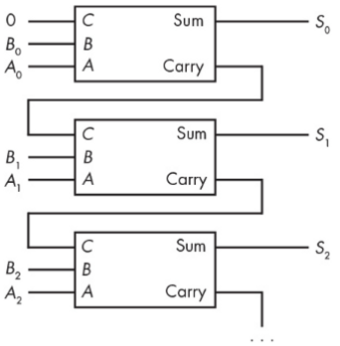
Ripple-carry Adder¶

full adder들을 순차적으로 연결하여 구현.

input carry가 이전 자리에 대한 full adder의 출력 carry와 연결됨.
각 full adder의 출력 carry가 다음 자리의 input으로 연결되어 각 비트에서 다음 비트로 물결이 출렁이듯 전달된다는 의미로 ripple이 붙음.

쉽게 이해가 되는 구조이나 propagation delay 등으로 인해 자리수가 높은 adder 구현에는 적합하지 않음.

Carry Look-ahead Adder¶

\(i+1\) th bit의 입력 carry (or carry-in)는 다음과 같이 \(i\) th bit의 입력 bit \(A_i,B_i\)와 carry-in \(C_i\)에 의해 결정됨.

\[ C_{i+1} = (A_i \text{ AND } B_i ) \text{ OR } (A_i \text{ AND } C_i ) \text{ OR }(B_i \text{ AND } C_i )\]

ripple carry adder의 문제점이 carry들이 순차적으로 입력되는 구조라는 점인데, 다음자리의 carry_in을 계산하려면 현재 자리의 carry-in이 있으면 되므로 이를 미리 계산해낼 수 있고,이 경우 맨 첫자리의 carry-in과 모든 자리의 \(A,B\)를 안다면 모든 자리의 carry-out을 구할 수 있다.

이를 위해,우선 \(i+1\) th bit의 입력 carry를 살펴보면 다음과 같은 식이 된다.

\[ C_{i+2} = (A_{i+1} \text{ AND } B_{i+1} ) \text{ OR } (A_{i+1} \text{ AND } C_{i+1} ) \text{ OR }(B_{i+1} \text{ AND } C_{i+1} ) \]

앞서 구한 \(C_{i+1}\)을 위 식에 대입하면, \(i+2\) th 의 carry-in (=\(i+1\) th carry-out)을 계산하는데, \(i\) th 의 입력정보만으로 충분함을 확인할 수 있다.

\[ \begin{aligned}C_{i+2} =& (A_{i+1} \text{ AND } B_{i+1} )\\& \text{ OR } (A_{i+1} \text{ AND } [(A_i \text{ AND } B_i ) \text{ OR } (A_i \text{ AND } C_i ) \text{ OR }(B_i \text{ AND } C_i )]) \\\\ &\text{ OR }(B_{i+1} \text{ AND } [(A_i \text{ AND } B_i ) \text{ OR } (A_i \text{ AND } C_i ) \text{ OR }(B_i \text{ AND } C_i )] )\end{aligned} \]

이를 가장 첫째 자리까지 수행하여 구하면 한번에 모든 자리의 carry를 구할 수 있게 된다.

이같이 carry를 구하는 방식의 adder를 carry look-ahead adder라고 부르며 이 경우 propagation delay의 영향이 최소화되게 된다. (단 더 많은 gate들이 필요함.)